II. NFA – Automata hữu hạn không đơn định

1. Định Nghĩa:

     Một Otomat hữu hạn không đơn định (NFA) là M= (Q, ∑, δ, q_o, F). Trong đó Q là một tập hơp hữu hạn các trạng thái, ∑ là bảng chữ - tập các ký tự vào,  q₀ là trạng thái bắt đầu , F là tập các trạng thái kết thúc (hay các trạng thái đoán nhận)  và δ là hàm chuyển đổi trạng thái  Q x ∑ → 2^Q.(Hàm này là sự khác nhau duy nhất giữa DFA và NFA).

     Hình miêu tả như sau:

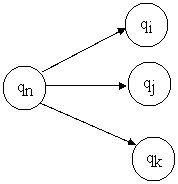
     Các thành phần của NFA gần như là giống các thành phần của DFA chỉ khác ở hàm chuyển đổi về số trạng thái mà Ôtomat có thể chuyển tới khi sử lí một kí tự đầu

 vào. Với DFA thì chỉ có một trạng thái được chuyển tới khi sử lí một kí tự vào từ  một trạng thái cho trước. Còn trong NFA thì có nhiều hơn một trạng thái có thể đến được từ một trạng thái cho trước khi xử lí một kí tự đầu vào. Và dễ thấy DFA là một trường hợp đặc biệt của NFA khi nó chỉ đi đến một trạng thái khác khi đọc một ký tự vào.

III .Sự Tương Đương Giữa DFA Và NFA   

  Ta sẽ thấy rằng sự mở rộng DFA thành NFA không tăng thêm khả năng đoán nhận ngôn ngữ. Giả sử L(DFA) và L(NFA) lần lượt trỏ lớp các ngôn ngữ đoán nhận được bởi các DFA và bởi các NFA .Vì theo định nghĩa một DFA cũng là một NFA, cho nên

                              L(DFA)    Í     L(NFA)                                  (*)

 Ta hãy xét theo chiều ngược lại.

  Định Lý 2.1: Nếu l là một ngôn ngữ được đoán nhận bởi một ÔHK thì cũng có một ÔHĐ đoán nhận L.

                                     Nói cách khác  L(NFA) Í  L(DFA)          (**)

  Hệ Quả 2.1:L(DFA)=L(NFA)

 Nói cách khác:lớp các ngôn ngữ đoán nhận bởi các ôtômát hữu hạn đơn định và lớp các ngôn ngữ đoán nhận bởi các ôtômát hữu hạn không đơn định là một.Gọi đó là các lớp ngôn ngữ chính qui ( viết tắt là lớp NNCQ ) .

 Chứng Minh Đinh Lí:

  Giả sử M = ( ∑ , Q , ∂, q_o, F ) là NFA đoán nhận L .

Thành lập DFA M’ = ( ∑, Q’,∂’ , q’_o , ,F’ ), trong đó :

    Q’ = 2 ^Q ; F’ là tập mọi trạng thái trong Q’ có chứa một trạng thái cuối nào đó của M . Mỗi phần tử trong Q’ được kí hiệu bởi  [ q_{1 ,} q₂ , q_{3 ,} ..., q­­_k ] với q_{1 ,} q₂ , ..., q_k 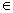 Q  .Trạng thái đầu q_o’ = [ q_o] .Hàm  chuyển ∂’ của M’ được thành lập theo công thức :

                        ∂’ ( [ q_{1 ,} q₂ ,..., q_k ] , a)= 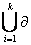(q_{1 ,}a)                                              (1)

Ta sẽ chứng minh L(M) = L(M’) .

• Trước hết chứng minh rằng : L(M) 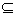 L(M’) ,tức là  chứng minh rằng nếu

                                                          w 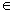 L(M)  thì  w  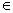L(M’);

 Với  w = a₁a₂ ...a_n , với  n 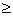 0 và có một suy dẫn trong M :

q₀ a₁a₂...a_{n 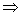  M} q₁a₂...a_{n 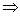M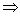}  ...  _M  q_n-1 a_{n 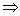 M}  q_n  với  q_n  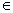F            (2)

 Cũng xâu  w đó  , đối với M’ sẽ có một suy dẫn  :

q’₀ a₁a₂...a_{n 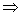  M’} q₁a₂...a_{n 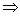M’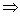}  ...  _M’  q_n-1 a_{n 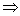 M’}  q’_n                          (3)

 Ta chứng minh bằng một qui nạp rằng :

         Với mọi i , 0  i    n  , q_i    q’_i                                                                 (4)

Hình : Các bước chuyển của M và M’

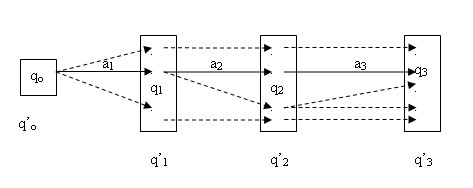
- Cơ sở qui nạp : q_o 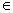 q_o’ bởi định nghĩa q_o’ = [ q_o] .

 - Bước qui nạp : Giả sử   đúng với i , tức là 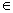q_i  q’_i

 Theo định nghĩa  của  suy dẫn trực tiếp ta  phải có :

             q_i+1 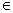 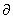 ( q_i , a_i+1)  và  q’_i+1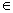 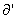  (q’_{i ,}a_i+1)

 Theo công thức (*) , thì nếu q_i 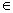q’_i  , ắt có :

                 ∂ (q_i ,a_i+1) 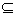 ∂( q’_i, a_i+1)

 Từ đó suy ra q_i 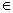 q’_i+1 , tức là (4) cũng đúng với  i+1 , kết thúc qui nạp .

 Từ (4) đã được chứng minh , suy ra  q_n 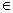q’_n .Nhưng q_n 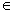F , suy ra: q’_n  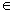F’ do định nghĩa  của F’ . Điều đó chứng tỏ w  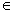L(M’) .

 Bây giờ chứng minh phần ngược lại : L(M’) 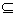 L(M) , tức là  chứng minh rằng nếu w  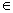L(M’)  thì  w  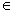L(M) .

         Giả sử có một suy dẫn trong M’ :

                           q’_o w 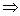^*_M’  q’ với  q’  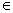 F’  

Trước hết hãy chứng minh   quy nạp theo độ dài  | w| rằng :

         Với mọi q 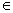 q’ , tồn tại suy dẫn trong M :

                                                                             q_o w 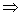_M  q                       (5)

- Cơ sở quy nạp  : Với | w | = 0 , tức w = 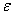 , do định nghĩa của quan hệ suy dẫn ta có

                                              q’_o 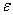 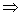 ^*_M’  q’_o

 Mặt khác  chỉ có q_o 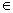 q’_o  và cũng  có  q_{o   M}  q_o

- Bước qui nạp :  Giả  thiết là  (5) đã đúng với các xâu có độ dài   | w | - 1 , hãy chứng minh  nó cũng đúng với xâu w

 Giả  sử w = xa , x 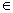∑^*, a 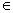 ∑  và  q’_o xa 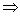^*_M’  p’ a 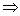^*_M’  q’ , trong đó ∂’( p’, a ) = q’

Xét một trạng thái bất kì q 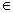 q’ . Do định nghĩa  của thì tồn tại p  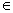p’ sao cho q  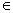∂(p , a) . Vậy theo giả  thiết qui nạp , tồn tại một suy dẫn trong M  q_o x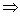a ^*_M  pa 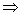^*_M  q , cho phép kết thúc sự qui nạp .

Trở lại giả thiết w 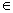 L(M’) , tức là q’_o w 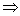^*_M’  q’ với q’  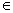F’ .

Vì  q’ 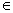 F’ , nên có q  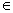q’ sao cho q  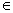F  .Vận dụng kết quả  vừa chứng minh có ngay    q_o w 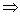^*_M  q ; vậy w  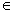L(M)  ,dẫn đến kết luận  L(M’)  L(M) .

 Kết  hợp hai kết quả đã chứng minh : ta có L(M) = L(M’)  và  định lí được chứng minh.

IV. Giải thuật để chuyển từ NFA-l sang loại DFA tương đương.

Lý thuyết:

      Ở  phần lý thuyết trên chúng ta đã đưa ra 3 loại Automat là DFA, NFA, NFA-l. Thấy rằng, mỗi loại sau là tổng quát của các trường hợp trước. Ở đây chúng ta sẽ xem xét  giải thuật để chuyển từ NFA-l sang loại DFA tương đương.

      Xét một NFA-l ta có như hình vẽ :

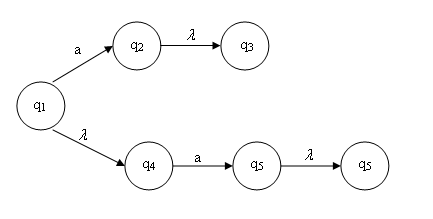
         Trong hình giá trị của t(q₁,a) = {q_2,q₃,q₄,q₅} trạng thái q₄ đạt tới khi không xử lí 1 kí tự nào ở đầu vào. 

          Hình dung, hàm chuyển đổi t(q_i,a) có thể chia ra làm 3 thành phần như sau:

    -  Đầu tiên là tập các trạng thái có thể đến được từ q_i mà không cần xử lí một kí tự nào cả

    -  Sau đó là các trạng thái có thể đến đựơc khi xử lí kí tự a từ các trạng thái trong tập các trạng thái trên.

    -  Cuối cùng theo các cung l từ các trạng thái kết quả trên để sinh ra tập t(q_i,a).

        Hàm t được định nghĩa trong thuật ngữ của hàm chuyển đổi d và đường đẫn trong biểu đồ trạng thái, nó đọc một xâu rỗng. Nút q_j là bao đóng của trạng thái q_i nếu có một đường từ q_i ® q_j mà đọc một xâu rỗng.

        Định nghĩa 1: Bao đóng l-closure của trạng thái q_i kí hiệu l-closure(q_i), được định nghĩa đẹ quy như sau

                     i)   Cơ sở: Trạng thái q_i thuộc l-closure(q_i) .

                     ii)  Giả thiết đệ quy: Giả sử q_j thuộc l-closure(q_i) . Nếu q_k thuộc d(q_j,l) thì q_k thuộc l-closure(q_i) 

                     iii) Kết luận : q_j thuộc vào l-closure(q_i) khi và chỉ khi nó có thể tới được từ q_i sau một  số hữu hạn  áp dụng các bước đệ quy

        Tập l-closure(q_i) có thể được tạo ra theo cách top-down approach trong giải thuật  4.3.1, nó quyết định dãy liên kết trong ngôn ngữ phi ngữ cảnh. Hàm chuyển đầu vào có thể tạo ra được từ l-closure(q_i) của các trạng thái và hàm chuyển đổi của NFA-l.

         Định nghĩa 2 : Hàm biến đổi đầu vào t của một NFA-l M là một hàm từ Q x å ® r(Q) bởi :

                   T(q_i,a)=U l-closure(q_i)  với q_j thuộc bao đóng của l-closure(q_i) và d là hàm chuyển đổi của M

      2 . Giải thuật :

       Giải thuật , xây dựng biểu đồ trạng thái của máy quyết định tương đương với một NFA -l M. Các nút của DFA, gọi là DM cho quyết định tương đương của M, là tập các nút của M. Nút bắt đầu của DM là bao đóng l-closure của bất kỳ nút nào trong các nút bắt đầu của M. Chìa khoá của giải thuật ở bước 2.1 . Nó sinh ra các nút của DM. Nếu X là nút của DM thì tập Y được tạo ra chứa toàn bộ các trạng thái có thể tới được bằng cách sử lí kí tự a từ tất cả các trạng thái trong X. Trong biểu đồ trạng thái của DM thì quan hệ này được thể hiện bằng một cung từ X ® Y với nhãn a. Nút X đuợc làm quyết định bằng cách tạo ra 1 cung từ nó tơi mọi kí tự trong bảng chữ. Một nút mới được sinh ra trong bước 2.1.1 đựơc thêm vào tập Q’ và quá trình tiếp tục cho tới khi mọi nts trong Q’ là quyết định được.

     Mã giải :

        Đầu vào :  cho  một NFA-l M=(Q,∑,δ,q₀,F) vào hàm dịch t của M.

        1. Chuẩn bị  Q' để l-closure(q₀).

        2. Repeat

                2.1. If  Có 1 nút X  Q’  và một ký tự a  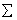 với  không có cung rời khỏi X mà được đánh nhãn là a

                        Then

                        2.1.1 Cho Y = .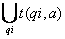

.                       2.1.2. If  Y 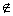 Q’, then  Q’ := Q’ U {Y}

                        2.1.3. Thêm một cung từ X vào Y nhãn là a.

                        Else   done := true

           Until done 

        3. Tập các  trạng thái đoán nhận của DM  là  F’ = { X 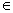 Q’ | X chưá  1 thành  phân q_i  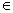F}