NGHIÊN CỨU THUẬT TOÁN SVM
XÂY DỰNG ỨNG DỤNG PHÂN CỤM DỮ LIỆU
Vấn đề phân lớp và dự đoán là khâu rất quan trọng trong học máy và trong khai phá dữ liệu, phát hiện trí thức. Kỹ thuật Support Vector Machines (SVM) được đánh giá là công cụ mạnh và tinh vi nhất hiện nay cho những bài toán phân lớp phi tuyến. Nhiều những ứng dụng đã và đang được xây dựng dựa trên kỹ thuật SVM rất hiệu quả
SVM là một phương pháp phân lớp hiện đại và hiệu quả, nắm chắc phương pháp này sẽ tạo nền tảng giúp chúng ta trong việc phát triển các giải pháp phân loại và dự đoán...,xây dựng được những ứng dụng quan trọng trong thực tế.
Ứng dụng phân lớp SVM cho bài toán phân cụm sinh viên là bài toán đã và
đang được nghiên cứu và phát triển rộng rãi và có ý nghĩa cả về học thuật lẫn ứng dụng thực tế.
Support Vector Machines (SVM) là kỹ thuật mới đối với việc phân lớp dữ liệu, là phương pháp học sử dụng không gian giả thuyết các hàm tuyến tính trên không gian đặc trưng nhiều chiều, dựa trên lý thuyết tối ưu và lý thuyết thống kê. Trong kỹ thuật SVM không gian dữ liệu nhập ban đầu sẽ được ánh xạ vào không gian đặc trưng và trong không gian đặc trưng này mặt siêu phẳng phân chia tối ưu sẽ được xác định. Ta có tập S gồm e các mẫu học S = {(x1,y1), (x2,y2), (x3,y3)…..( xe,ye)} (X x Y)e với một vectơ đầu vào n chiều xi ∈ Rn thuộc lớp I hoặc lớp II (tương ứng nhãn y i =1 đối với lớp I và y i= - 1 đối với lớp II). Một tập mẫu học được gọi là tầm thường nếu tất cả các nhãn là bằng nhau.
Đối với các dữ liệu phân chia tuyển tính, chúng ta có thể xác định được siêu phẳng f(x) mà nó có thể chia tập dữ liệu. Khi đó, với mỗi siêu phẳng nhận được ta có: f(x)≥ 0 nếu đầu vào x thuộc lớp dương, và f(x)< 0 nếu x thuộc lớp âmf(x) = w.x +b, trong đó w là vector pháp tuyến n chiều và b là giá trị ngưỡng. Vector pháp tuyến w xác định chiều của siêu phẳng f(x), còn giá trị ngưỡng bxác định khoảng cách giữa siêu phẳng và gốc.Siêu phẳng có khoảng cách với dữ liệu gần nhất là lớn nhất (tức có biên lớn nhất) được gọi là siêu phẳng tối ưu.
Mục đích đặt ra ở đây là tìm được một ngưỡng (w,b) phân chia tập mẫu vào các lớp có nhãn 1 (lớp I) và -1 (lớp II) nêu ở trên với khoảng cách là lớn nhất.
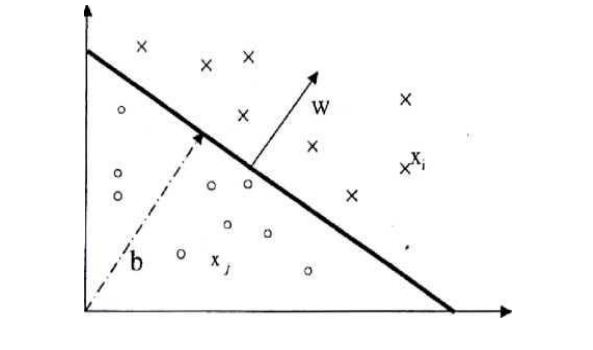
Hình 1.1 Phân tách theo siêu phẳng (w,b) trong không gian 2 chiều của tập mẫu
Siêu phẳng có khoảng cách với dữ liệu gần nhất là lớn nhất (tức có biên lớn nhất) được gọi là siêu phẳng tối ưu.
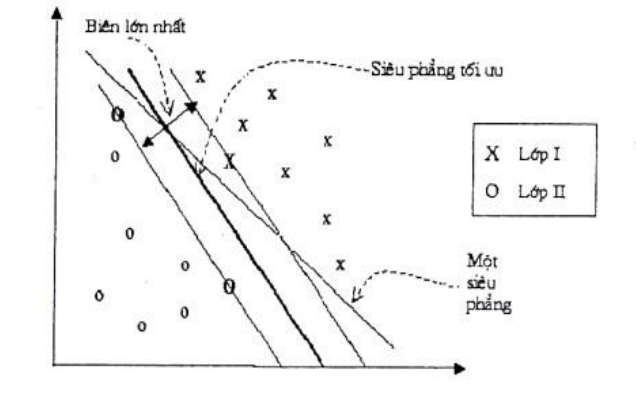
Phân lớp dữ liệu là một kỹ thuật trong khai phá dữ liệu được sử dụng rộng rãi nhất và được nghiên cứu mở rộng hiện nay.
Mục đích: Để dự đoán những nhãn phân lớp cho các bộ dữ liệu hoặc mẫu mới.
Đầu vào: Một tập các mẫu dữ liệu huấn luyện,với một nhãn phân lớp
cho mỗi mẫu dữ liệu.
Đầu ra: Bộ phân lớp dựa trên tập huấn luyện,hoặc những nhãn phân lớp.
Phân lớp dữ liệu dựa trên tập huấn luyện và các giá trị trong một thuộc tính phân lớp và dùng nó để xác định lớp cho dữ liệu mới. Kỹ thuật phân lớp dữ liệu được tiến hành bao gồm 2 bước:
Bước 1. Xây dựng mô hình từ tập huấn luyện
- Mỗi bộ/mẫu dữ liệu được phân vào một lớp được xác định trước.
- Lớp của một bộ/mẫu dữ liệu được xác định bởi thuộc tính gán nhãn lớp.
- Tập các bộ/mẫu dữ liệu huấn luyện - tập huấn luyện - được dùng để xây dựng mô hình.
- Mô hình được biểu diễn bởi các luật phân lớp,các cây quyết định hoặc các công thức toán học.

Bước 2: Sử dụng mô hình – kiểm tra tính đúng đắn của mô hình và dung nó để phân lớp dữ liệu mới.
- Phân lớp cho những đối tượng mới hoặc chưa được phân lớp.
- Đánh giá độ chính xác của mô hình Lớp biết trước của một mẫu/bộ dữ liệu đem kiểm tra được so sánh với kết quả thu được từ mô hình. Tỉ lệ chính xác bằng phần trăm các mẫu/bộ dữ liệu được phân lớp đúng bởi mô hình trong số các lần kiểm tra.
- SVM rất hiệu quả để giải quyết bài toán dữ liệu có số chiều lớn (ảnh của dữ liệu biểu diễn gene, protein, tế bào).
- SVM giải quyết vấn đề overfitting rất tốt (dữ liệu có nhiễu và tách rời nhóm hoặc dữ liệu huấn luyện quá ít).
- Là phương pháp phân lớp nhanh.
- Có hiệu suất tổng hợp tốt và hiệu suất tính toán cao.
Bài toán phân lớp (Classification) và dự đoán (Prediction) là hai bài toán cơ bản và có rất nhiều ứng dụng trong tất cả các lĩnh vực như: học máy, nhận dạng, trí tuệ nhân tạo, .v.v . Trong đồ án này, chúng em sẽ đi sâu nghiên cứu phương pháp Support Vector Machines (SVM), một phương pháp rất hiệu quả hiện nay.
Phương pháp SVM được coi là công cụ mạnh cho những bài toán phân lớp phi tuyến tính được các tác giả Vapnik và Chervonenkis phát triển mạnh mẽ năm 1995.
Phương pháp này thực hiện phân lớp dựa trên nguyên lý Cực tiểu hóa rủi ro có Cấu trúc SRM (Structural Risk Minimization), được xem là một trong các phương pháp phân lớp giám sát không tham số tinh vi nhất cho đến nay. Các hàm công cụ đa dạng của SVM cho phép tạo không gian chuyên đổi để xây dựng mặt phẳng phân lớp.
Là phương pháp dựa trên nền tảng của lý thuyết thống kê nên có một nền tảng toán học chặt chẽ để đảm bảo rằng kết quả tìm được là chính xác.
Là thuật toán học giám sát (supervied learning) được sử dụng cho phân lớp dữ liệu.
Là 1 phương pháp thử nghiệm, đưa ra 1 trong những phương pháp mạnh và chính xác nhất trong số các thuật toán nổi tiếng về phân lớp dữ liệu.
SVM là một phương pháp có tính tổng quát cao nên có thể được áp dụng cho nhiều loại bài toán nhận dạng và phân loại.
Cho trước một tập huấn luyện, được biểu diễn trong không gian vector, trong
đó mỗi tài liệu là một điểm, phương pháp này tìm ra một siêu phẳng quyết định tốt nhất có thể chia các điểm trên không gian này thành hai lớp riêng biệt tương ứng là lớp + và lớp -.
Chất lượng của siêu phẳng này được quyết định bởi khoảng cách (gọi là biên) của điểm dữ liệu gần nhất của mỗi lớp đến mặt phẳng này. Khi đó, khoảng cách biên càng lớn thì mặt phẳng quyết định càng tốt, đồng thời việc phân loại càng chính xác.
Mục đích của phương pháp SVM là tìm được khoảng cách biên lớn nhất,
điều này được minh họa như sau:
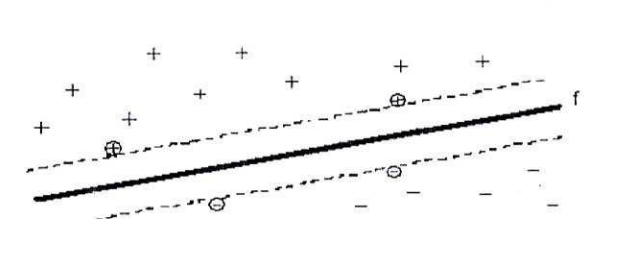
Hình 1 5: Siêu phẳng chia dữ liệu thành 2 lớp + và - với khoảng cách biên lớn nhất.
Các điểm gần nhất (điểm được khoanh tròn) là các Support Vector.
SVM thực chất là một bài toán tối ưu, mục tiêu của thuật toán này là tìm được một không gian F và siêu phẳng quyết định f trên F sao cho sai số phân loại là thấp nhất.
Cho tập mẫu (x1, y1), (x2, y2), … (xf, y f)} với xi ∈ Rn , thuộc vào hai lớp nhãn: yi ∈ {-1,1} là nhãn lớp tương ứng của các xi (-1 biểu thị lớp I, 1 biểu thị lớp II).
Ta có, phương trình siêu phẳng chứa vectơ xi trong không gian:
xi .w + b = 0 +1, Xi . W + b > 0
Đặt f(Xi) = sign (Xi . W + b) = -1, Xi . W + b < 0
Như vậy, f(Xi) biểu diễn sự phân lớp của Xi vào hai lớp như đã nêu. Ta nói yi= +1 nếu Xi € lớp I và yi = -1 nếu Xi € lớp II . Khi đó, để có siêu phẳng f ta sẽ phải giải bài toán sau:
Tìm min với W thỏa mãn điều kiện sau: yi(sin (Xi.W + b)) ≥ 1 với i € 1,n.
Bài toán SVM có thể giải bằng kỹ thuật sử dụng toán tử Lagrange để biến đổi về thành dạng đẳng thức. Một đặc điểm thú vị của SVM là mặt phẳng quyết định chỉ phụ thuộc các Support Vector và nó có khoảng cách đến mặt phẳng quyết định là 1/. Cho dù các điểm khác bị xóa đi thì thuật toán vẫn cho kết quả giốngnhư ban đầu. Đây chính là điểm nổi bật của phương pháp SVM so với các phương pháp khác vì tất cả các dữ liệu trong tập huấn luyện đều được đùng để tối ưu hóa kết quả.
TÓM LẠI:
Trong trường hợp nhị phân phân tách tuyến tính, việc phân lớp được thực hiện qua hàm quyết định f(x) = sign(<w.x> + b), hàm này thu được bằng việc thay đổi vectơ chuẩn w, đây là vectơ để cực đại hóa viền chức năng.
Việc mở rộng SVM để phân đa lớp hiện nay vẫn đang được đầu tư nghiên cứu. Có một phương pháp tiếp cận để giải quyết vấn để này là xây dựng và kết hợp nhiều bộ phân lớp nhị phân SVM (Chẳng hạn: trong quá trình luyện với SVM, bài toán phân m lớp có thể được biến đổi thành bài toán phân 2*m lớp, khi đó trong mỗi hai lớp, hàm quyết định sẽ được xác định cho khả năng tổng quát hóa tối đa).
Trong phương pháp này có thể đề cập tới hai cách là một-đổi-một, một-đối-tất cả.
Bài toán đặt ra là: Xác định hàm phân lớp để phân lớp các mẫu trong tương
lai, nghĩa là với một mẫu dữ liệu mới xi thì cần phải xác định xi được phân vào lớp +1 hay lớp -1.
Để xác định hàm phân lớp dựa trên phương pháp SVM, ta sẽ tiến hành tìm hai siêu phẳng song song sao cho khoảng cách y giữa chúng là lớn nhất có thể để phân tách hai lớp này ra làm hai phía. Hàm phân tách tương ứng với phương trình siêu phẳng nằm giữa hai siêu phẳng tìm được.
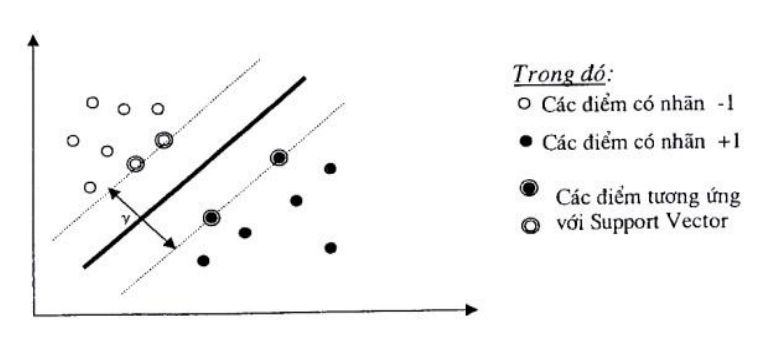
Các điểm mà nằm trên hai siêu phẳng phân tách được gọi là các Support
Vector. Các điểm này sẽ quyết định đến hàm phân tách dữ liệu.
Để phân nhiều lớp thì kỹ thuật SVM nguyên thủy sẽ chia không gian dữ liệu thành 2 phần và quá trình này lặp lại nhiều lần. Khi đó hàm quyết định phân dữ liệu vào lớp thứ i của tập n , 2-Iớp sẽ là: fi(x) = wi.xi + bi
Những phần tử x là support vector sẽ thỏa điều kiện +1 nếu thuộc lớp i
fi (x) = -1 nếu thuộc phần còn lại.
Như vậy, bài toán phân nhiều lớp sử dụng phương pháp SVM hoàn toàn có thể thực hiện giống như bài toán hai lớp. Bằng cách sử dụng chiến lược "một- đốimột”(one - against - one). Giả sử bài toán cần phân loại có k lớp (k > 2), chiến lược "một-đối-một”sẽ tiến hành k(k-l)/2 lần phân lớp nhị phân sử dụng phương pháp SVM. Mỗi lớp sẽ tiến hành phân tách với k-1 lớp còn lại để xác định k-1 hàm phân tách dựa vào bài toán phân hai lớp bằng phương pháp SVM.
Phương pháp SVM yêu cầu dữ liệu được diễn tả như các vector của các số thực. Như vậy nếu đầu vào chưa phải là số thì ta cần phải tìm cách chuyển chúng về dạng số của SVM Tiền xử lý dữ liệu: Thực hiện biến đổi dữ liệu phù hợp cho quá trình tính toán, tránh các số quá lớn mô tả các thuộc tính. Thường nên co giãn (scaling) dữ liệu để chuyển về đoạn [-1, 1] hoặc [0, 1].
Chọn hàm hạt nhân: Lựa chọn hàm hạt nhân phù hợp tương ứng cho từng bài toán cụ thể để đạt được độ chính xác cao trong quá trình phân lớp. Thực hiện việc kiểm tra chéo để xác định các tham số cho ứng dụng.
Điều này cũng quyết định đến tính chính xác của quá trình phân lớp. Sử dụng các tham số cho việc huấn luyện với tập mẫu.
Trong quá trình huấn luyện sẽ sử dụng thuật toán tối ưu hóa khoảng cách giữa các siêu phẳng trong quá trình phân lớp, xác định hàm phân lớp trong không gian đặc trưng nhờ việc ánh xạ dữ liệu vào không gian đặc trưng bằng cách mô tả hạt nhân, giải quyết cho cảhaitrường hợp dữ liệu là phân tách và không phân tách tuyến tính trong không gian đặc trưng.
Kiểm thử tập dữ liệu Test.
Trong lĩnh vực khai phá dữ liệu, các phương pháp phân lớp văn bản đã dựa trên những phương pháp quyết định như quyết định Bayes, cây quyết định, k-người láng giềng gần nhất, …. Những phương pháp này đã cho kết quả chấp nhận được và được sửdụng nhiều trong thực tế. Trong những năm gần đây, phương pháp phân lớp sử dụng tập phân lớp vector hỗ trợ (máy vector hỗ trợ - Support Vector Machine – SVM) được quan tâm và sử dụng nhiều trong lĩnh vực nhận dạng và phân lớp. SVM là một họ các phương pháp dựa trên cơ sở các hàm nhân (kernel) để tối thiểu hoá rủi ro ước lượng. Phương pháp SVM ra đời từ lý thuyết học thống kê do Vapnik và Chervonenkis xây dựng và có nhiều tiềm năng phát triển về mặt lý thuyết cũng như ứng dụng trong thực tiễn. Các thử nghiệm thực tế cho thấy, phương pháp SVM có khả năng phân lớp khá tốt đối với bài toán phân lớp văn bản cũng như trong nhiều ứng dụng khác (như nhận dạng chữ viết tay, phát hiên mặt người trong các ảnh, ước lượng hồi quy,…). Xét với các phương pháp phân lớp khác, khả năng phân lớp của SVM là tương đối tốt và hiệu quả.
Ngày nay, việc phân cụm sinh viên theo điểm trung bình các môn hay điểm trung bình học kì là rất quan trọng. Dựa vào việc phân loại này, giảng viên sẽ biết được tình trạng lớp học của mình để có thể thay đổi phương pháp giảng dạy hiệu quả nhất, hay có thể hướng dẫn sinh viên chọn chuyên ngành phù hợp hay chọn môn học tự chọn nào để có thể đạt kết quả cao nhất. Về phía sinh viên, sinh viên có thể tự đánh giá năng lực học của mình để tự lựa chọn chuyên ngành thích hợp, sinh viên có thể biết mình đang học ở mức độ nào trong lớp để phấn đấu đạt kết quả học tập tốt hơn.
Thấy được sự cần thiết đó, chúng em đã xây dựng một chương trình ứng dụng giúp phân cụm sinh viên theo điểm trung bình để làm giảm bớt những khó khăn trong việc quản lý sinh viên và cũng giúp các bạn sinh viên có hướng đi đúng đắn cho mình.
Việc phân cụm theo điểm trung bình chia làm 2 cách: phân 2 cụm (dựa trên SVM nhị phân) và phân đa cụm (dựa trên SVM đa cụm).
Ý tưởng của bài toán này là phân điểm trung bình của sinh viên ra làm 2 cụm, cụm 1 là dưới 5 điểm, cụm 2 là trên 5 điểm (Lấy chuẩn đậu và rớt thông thường để chia). Lấy MAX( cụm 1) và MIN( cụm 2), tiếp tục lấy trung bình cộng của MAX, MIN đó (gọi là ngưỡng), lấy từng điểm trung bình của sinh viên đem so sánh với ngưỡng đó để phân chia điểm đó thuộc bờ bên nào của ngưỡng (nhỏ hơn hay lớn hơn ngưỡng). Như vậy chúng ta có thể phân chia điểm trung bình của sinh viên thành 2 cụm một cách nhanh chóng.
Cũng tương tự như phân 2 cụm, chúng ta phân điểm trung bình của sinh viên theo số cụm mà người dùng nhập vào, qua đó ta xác định được mức độ học tập của lớp đó theo từng mức điểm khác nhau. Ý tưởng của việc phân cụm này dựa vào ý tưởng của phân 2 cụm ở trên. Ban đầu ta lấy số điểm tối đa của điểm ( 10 điểm) chia cho số cụm muốn phân chia, sau đó ta tính MAX, MIN hai bên bờ của từng khoảng điểm đó, sau đó ta lại tiếp tục lấy trung bình của MAX, MIN để tìm ra điểm ngưỡng của từng khoảng (số các khoảng là số cụm muốn chia). Duyệt qua danh sách điểm trung bình để phân chia điểm đó thuộc vào khoảng nào. Theo cách làm trên, ta sẽ phân chia điểm trung bình của sinh viên theo số cụm mong muốn.
Đối với phương pháp phân cụm nhị phân, chương trình phân cụm một cách khá chính xác. Nhưng với phương pháp phân đa cụm thì kết quả không chính xác khi số cụm quá lớn, do tập dữ liệu phân cụm ít nên việc phân ra quá nhiều cụm không đảm bảo chính xác, có một số cụm số phần tử là 0 và cũng có cụm số phần tử chiếm tỉ lệ cao. Do đó đòi hỏi tập dữ liệu đầu vào phải tốt cho việc phân đa cụm.