KHAI THÁC TẬP HỮU ÍCH CAO TRÊN CƠ SỞ DỮ LIỆU BÁN HÀNG SIÊU THỊ BẰNG THUẬT TOÁN FHM

Thuật toán FHM

Các khái niệm liên quan

Cơ sở dữ liệu giao dịch là gì ?

Một giao dịch, lấy bối cảnh ở trong CSDL là đơn vị logic được thực hiện độc lập để truy xuất hoặc cập nhật dữ liệu. Trong CSDL quan hệ, các CSDL giao dịch phải nguyên tử, nhất quán, tách biệt và bền. viết tắt là ACID.

Các giao dịch được hoàn thành bằng các câu lệnh SQL COMMIT (xác nhận) hoặc ROLLBACK (khôi phục), để chỉ ra giao dịch bắt đầu hay kết thúc. Các tính chất của một CSDL giao dịch được định nghĩa như sau:

• • Tính nguyên tử: một giao dịch phải hoàn thành đầy đủ, được lưu trữ (được xác nhận) hoặc hoàn thành hoàn tác (khôi phục). Việc bán hàng trong CSDL bán hàng riêng lẻ minh họa cho kịch bản để giải thích tính nguyên tử. Ví dụ, việc bán hàng bao gồm giảm số lượng hàng tồn và nhận tiền đang đến. Cả hai xảy ra đồng thời hoặc không xảy ra - nó là tất cả hoặc không là gì.
  • Tính nhất quán: giao dịch phải được tuân thủ đầy đủ trạng thái của CSDL như trước giao dịch. Nói cách khác, giao dịch không thể phá vỡ các ràng buộc của CSDL. CD, nếu cột Number Phone của CSDL chỉ có thể các chữ số, khi đó tính nhất quán chỉ ra rằng mọi giao dịch cố gắng nhập chữ cái có thể không được xác nhận.
  • Tính tách biệt: Dữ liệu giao dịch phải không được có sẵn từ CSDL khác cho đến khi giao dịch ban đầu được xác nhận hoặc khôi phục.
  • Tính bền: Thay đổi dữ liệu giao dịch phải được có sẵn. ngay cả trong trường hợp CSDL bị lỗi.

Item, Itemset

Tồn tại một lượng lớn các dữ liệu mã quét được thu thập từ nhiều doanh nghiệp, nó thể hiện rằng một kho thông tin tiềm năng được cung cấp các phương thức đầy đủ (thích hợp) để chuyển đổi dữ liệu thành thông tin có ý nghĩa. Một loại dữ liệu như vậy được lưu trữ trong CSDL giao dịch từ đó tất cả các mặt hàng thu được trong CSDL riêng lẻ có thể truy xuất như một đơn vị. Các giao dịch khi đó có thể được kiểm tra để xác định mặt hàng nào thường xuất hiện cùng nhau, tức là, các mặt hàng khách hàng thường mua cùng nhau trong CSDL của giao dịch siêu thị. Điều này lần lượt cho ta cái nhìn sâu sắc về các câu hỏi như làm cách nào tiếp thị các sản phẩm hiệu quả hơn, làm cách nào nhóm chúng trong việc bố trí cửa hàng và đóng gói sản phẩm, hoặc mặt hàng nào sẽ được chào bán để tăng cường bán các mặt hàng khác.

Nghiên cứu gần đây đã tập trung xác định nhóm các item nào thường xuyên xuất hiện cùng nhau trong các giao dịch, gọi là itemset. Từ bất kỳ itemset, một quy tắt liên kết được rút ra, biết được tần suất xuất hiện của tập con các item trong itemset, thì có thể dự đoán xác suất xảy ra của các item còn lại. Một số thuật toán đã được đề xuất để tìm kiếm các itemset tổng quát từ các item được phân lớp theo một hoặc nhiều phân cấp phân loại (taxonomic heirarchies).

Một tổ chức bán lẻ có thể cung cấp hàng ngàn sản phẩm và dịch vụ. Số kết hợp có thể có của các sản phẩm và dịch vụ này là vô cùng lớn. Trong các trường hợp chung, để kiểm tra tất cả số kết hợp có thể có là không khả thi và các phương thức được yêu cầu cố gắng tập trung vào các itemset được xem là quan trọng từ tổ chức. Thông thường nhất được sử dụng để đo tầm quan trọng của một itemset là support, nó là tỷ lệ phần trăm của tất cả các giao dịch có chứa itemset. Một quy tắc kết hợp của mẫu A → B(trong đó A và B là các itemset) được liên kết với một thước đo tin cậy là tỷ lệ giữa support của itemset A U B và support của itemset A. Độ tin cậy định lượng xác suất khi A được mua thì B cũng sẽ được mua.

Các itemset đáp ứng được ngưỡng support tối thiểu thì được xem là itemset thường xuyên. Lý do đằng sau để sử dụng support là để tổ chức bán lẻ chỉ cần quan tâm các itemset này có thường xuyên xảy ra. Tuy nhiên, support chỉ nói đến số giao dịch trong đó itemset đã được mua. Số lượng mặt hàng chính xác được mua không được phân tích và tác động chính xác của việc mua một mặt hàng có thể không được đo lường như về mặt tồn kho, chi phí và lợi nhuận. Sự thiếu sót này của việc đo lường support đã thúc đẩy sự phát triển của một độ đo có tên gọi là itemset share, phần nhỏ của một vài giá trị số, như là tổng số lượng các item được mua hoặc tổng lợi nhuận, được đóng góp bởi các item khi chúng xảy ra trong một itemset. Nhìn chung, các đo lường dựa trên share cung cấp nhiều thông tin bất kể khi nào các item được mua theo bội số.

Các định nghĩa và công thức

Định nghĩa 1: (Cơ sở dữ liệu giao dịch). Đặt I là một tập hợp các mục. Cơ sở dữ liệu giao dịch là một tập hợp các giao dịch, ký hiệu D = { T₁,  T₂, ..., T_n} sao cho mỗi giao dịch T_c vớiT_c ∈ I và T_c có một định danh duy nhất được gọi là Tid. Mỗi mục i ∈ I được liên kết với một số dương p(i), được gọi là tiện ích bên ngoài của nó (ví dụ: đơn vị lợi nhuận).  Mỗi mục i ∈T_c có mộtsố dương q (i, T_c) được gọi là độ hữu ích nội bộ của i (ví dụ: số lượng mua).[6]

Ví dụ 1. Xét cơ sở dữ liệu của Hình 2.1 (bên trái), cơ sở dữ liệu giao dịch này sẽ được sử dụng làm ví dụ chạy của thuật toán. Cơ sở dữ liệu này chứa các giao dịch ( T₁,  T₂ ...  T₅). Giao dịch T₂ chỉ ra rằng các mục a, c, e và g xuất hiện trong giao dịch này với độ hữu ích nội bộ tương ứng là 2, 6, 2 và 5. Hình 2.1 (bên phải) chỉ ra rằng độ hữu ích bên ngoài của các mục này tương ứng là 5, 1, 3 và 1.

Hình 2. 1 Cơ sở dữ liệu giao dịch ( bên trái) và các giá trị tiện ích bên ngoài ( bên phải)

Định nghĩa 2: (Độ hữu ích của một mục trong một giao dịch). Tiện ích của một mục i trong giao dịch T_c được ký hiệu là u (i, T_c) và được định nghĩa là p(i) × q(i, T_c). Tiện ích của một itemset X trong giao dịch được ký hiệu là u (X, T_c) và được định nghĩa là u (X, T_c) = ∑_i∈X  u (i, T_c). [6]

Ví dụ 2. Độ hữu ích của mục a trong T₂ là u (a, T₂) = 5 × 2 = 10. Độ hữu ích của mục {a, c} trong T₂ là u ({a, c}, T₂) = u ( a, T₂) + u (c, T₂) = 5 × 2 + 1 × 6 = 16.

Định nghĩa 3: (Độ hữu ích của một mục trong cơ sở dữ liệu). Độ hữu ích của itemset X trong cơ sở dữ liệu D được ký hiệu là u( X ) và được định nghĩa là u( X ) = ∑ _{Tc∈g( X )} u( X, T_c ), trong đó g (X) là tập hợp các giao dịch có chứa X. [6]

Ví dụ 3. Độ hữu ích của các mục {a, c} là u ({a, c}) = u (a) + u (c) = u (a, T₁) + u (a, T₂) + u (a , T₃) + u (c, T₁) + u (c, T₂) + u (c, T₃) = 5 + 10 + 5 + 1 + 6+ 1 = 28.

Định nghĩa 4: ( Định nghĩa vấn đề). Một itemset X là một tập hữu ích cao nếu u(X) không nhỏ hơn ngưỡng tiện ích tối thiểu minutil (minimum utility threshold) do người dùng quy định. Ngược lại, X không phải là một tập hữu ích cao. [6]

Ví dụ 4. Nếu minutil = 30, các mục độ hữu ích cao trong cơ sở dữ liệu của ví dụ đang chạy  là {b, d}, {a, c, e}, {b, c, d}, {b, c, e} , {b, d, e}, {b, c, d, e} với một độ hữu ích tương ứng là 30, 31, 34, 31, 36, 40 và 30.

            Định nghĩa 5: (Transaction Utility). Độ hữu ích giao dịch (TU) của giao dịch T_c là tổng số độ hữu ích của các mục từ T_c trong T_c. tức là TU (T_c) = ∑ _x∈Tc u (x, Tc).

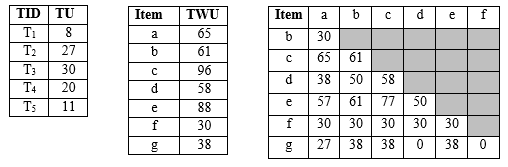
Hình 2. 2 Các tiện ích giao dịch ( bên trái ), giá trị TWU ( giữa ) và EUCS ( bên phải)

Ví dụ 5. Hình 2.2 (bên trái) hiển thị TU của các giao dịch T₁, T₂, T₃, T₄, T₅ từ ví dụ đang chạy.

            Định nghĩa 6: (Transaction Weighted Utilization). Transaction Weighted Utilization (TWU) của một itemset X được định nghĩa là tổng của độ hữu ích giao dịch của các giao dịch có chứa X, tức là TWU (X) = ∑ _{Tc ∈ g(X)} TU (T_c). [6]

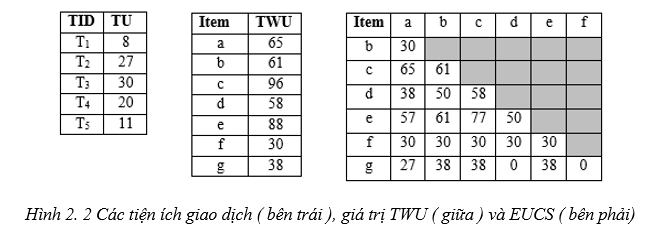Ví dụ 6. Hình 2.2 (giữa) hiển thị TWU của các mục đơn a, b, c, d, e, f, g. Xét mục a. Ta có: TWU (A) = TU (T₁) + TU (T₂) + TU (T₃) = 8 + 27 + 30 = 65

            Thước đo TWU có ba thuộc tính quan trọng được sử dụng để cắt tỉa không gian tìm kiếm.

Tính chất 1 (Overestimation). TWU của một itemset X cao hơn hoặc bằng độ hữu ích của nó, tức là TWU (X) ≥ u (X). [6]

Tính chất 2 (Antimonotonicity). Biện pháp TWU là chống đơn điệu. Xét 2 itemset X và Y. Nếu X Ì Y, thìTWU (X) ≥ TWU (Y). [6]

Tính chất (Pruning). Xét X là một mục. Nếu TWU (X) <minutil, thì bộ dữ liệu X là một itemset độ hữu ích thấp cũng như tất cả các siêu bộ của nó( chứng minh dựa vào tính chất 1 và tính chất 2). [6]

            Các thuật toán như Two-Phase, IHUP và UPGrowth sử dụng các thuộc tính đã nói ở trên để cắt tỉa không gian tìm kiếm. Chúng hoạt động theo hai giai đoạn. Trong giai đoạn 1, chúng xác định các mục độ hữu ích cao bằng cách tính TWU của chúng. Trong giai đoạn 2, chúng quét cơ sở dữ liệu để tính toán độ hữu ích chính xác của tất cả các ứng cử viên được tìm thấy trong Giai đoạn 1 để loại bỏ các mục độ hữu ích thấp. Gần đây, một cách tiếp cận khác đã được đề xuất trong thuật toán HUI-Miner để khai thác trực tiếp các mục độ hữu ích cao bằng cách sử dụng một pha. HUI-Miner đã được chứng minh là vượt trội hơn các thuật toán trước đó và là thuật toán tốt nhất tại thời điểm này. HUI-Miner sử dụng tìm kiếm đầu tiên chuyên sâu để khám phá không gian tìm kiếm của các mục và liên kết một cấu trúc có tên là danh sách độ hữu ích với mỗi mẫu. Danh sách độ hữu ích cho phép tính toán độ hữu ích của mẫu một cách nhanh chóng bằng cách thực hiện các hoạt động nối với danh sách độ hữu ích của các mẫu nhỏ hơn. Danh sách độ hữu ích được định nghĩa như sau.

            Định nghĩa 7: ( Utility-list). Đặt ≻ là thứ tự toàn phần các mục trong tập I. Utility-list của một mục X trong cơ sở dữ liệu D là một tập các bộ có cấu trúc (tid, iutil, rutil) cho mỗi giao dịch Tid chứa X. Phần tử iutil của một bộ là độ hữu ích của X trong T_tid. tức là u(X, T_tid). Phần tử rutil của một bộ được định nghĩa là ∑_{i∈Ttid ∧ i ∉ X} U(i, T_tid). [6]

 Ví dụ 7. Utility-list của {a} là {(T₁,5,3) (T₂,10,17) (T₃,5,25)}. Utility-list của {e} là {(T₂,6,5) (T₃,3,5) (T₄,3,0)}. Utility-list của {a, e} là {(T₂,16,5), (T₃,8,5)}.

            Để khám phá các tập mục có độ hữu ích cao, HUI-Miner thực hiện quét cơ sở dữ liệu một lần duy nhất để tạo các Utility-list có chứa các mục đơn. Sau đó, các mẫu lớn hơn thu được bằng cách thực hiện thao tác nối các độ hữu ích - danh sách các mẫu nhỏ hơn. Cắt bớt không gian tìm kiếm được thực hiện bằng hai thuộc tính sau.

Tính chất 4 (Tổng của  Iutils). Đặt X là một tập mục. Nếu tổng các giá trị iutil trong danh sách độ hữu ích của X cao hơn hoặc bằng minutil, thì X là một tập mục có độ hữu ích cao. Mặt khác, nó là một tập mục độ hữu ích thấp. [6]

Tính chất 5 (Tổng Iutils và Rutils). Đặt X là một tập mục. Đặt các phần mở rộng của X là các tập mục có thể thu được bằng cách nối thêm một mục y vào X sao cho y ≻ i cho tất cả các mục i trong X. Nếu tổng giá trị iutil và rutil trong utility-list của x nhỏ hơn minutil , tất cả các phần mở rộng của X và các phần mở rộng bắc cầu của chúng là các mục độ hữu ích thấp. [6]

HUI-Miner là một thuật toán rất hiệu quả. Tuy nhiên, một nhược điểm là thao tác nối để tính toán utility-list của một mục rất tốn kém. Trong phần tiếp theo sẽ giới thiệu thuật toán mới, cải thiện HUI-Miner bằng cách loại bỏ các mục độ hữu ích thấp mà không cần thực hiện kết hợp.

Thuật toán FHM

Thuật toán 1. Thuật toán FHM  [6]

Dữ liệu đầu vào : D: cơ sở dữ liệu giao dịch D, độ hữu ích tối thiểu minutil do người dùng chỉ định.

Dữ liệu đầu ra : Bộ itemsets hữu ích cao

1 Quét D, tính TWU của từng item riêng lẻ;

2 Với mỗi item i trong I* phải đảm bảo rằng TWU(i) < minutil;

3 Đặt là thứ tự toàn phần ( total order) tăng dần giá trị của TWU trong I*;

4 Quét D để xây dựng utility-list của mỗi item i thuộc i ∈ I* and xây dựng cấu trúc      EUCS;

5 Search (∅, I*, minutil, EUCS);

Trong phần này, thuật toán FHM sẽ được trình bày một cách chi tiết. Quy trình chính (tính chất 1) lấy đầu vào là cơ sở dữ liệu giao dịch với các giá trị độ hữu ích và ngưỡng minutil. Thuật toán đầu tiên quét cơ sở dữ liệu để tính TWU của từng item( mục). Sau đó, thuật toán xác định tập hợp I^* của tất cả các item có TWU không nhỏ hơn ngưỡng minutil mong muốn(các item khác bị bỏ qua vì chúng không thể là một phần của các item có độ hữu ích cao dựa vào tính chất 3). Các giá trị TWU của các item sau đó được sử

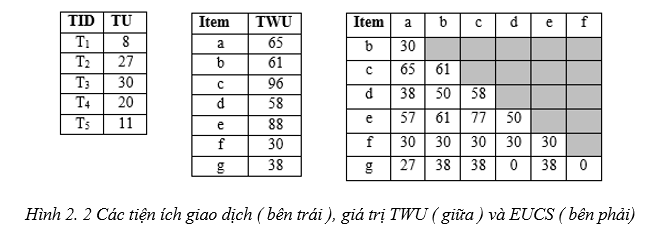dụng để thiết lập thứ tự toàn phần ( total order) ≻ cho các item, là thứ tự tăng dần các giá trị TWU (như được đề xuất ở tính chất 4 và 5). Sau đó thực hiện quét CSDL lần 2, trong lần quét này, các item trong giao dịch được sắp xếp lại theo tổng thứ tự ≻, danh sách độ hữu ích của từng mục i ∈ I^* được xây dựng và cấu trúc mới của chúng tôi có tên EUCS (Estimated Utility Co-Occurrence Structure) được xây dựng. Cấu trúc thứ hai này được định nghĩa là một bộ ba dạng có dạng (a, b, c) ∈ I^* × I^* × R. Một bộ ba (a, b, c) chỉ ra rằng TWU ({a, b}) = c ( ví dụ: bộ 3 được biểu diễn ( a, b, 30), trong đó a, b là các item, c = TWU ({a, b}) trong D). EUCS có thể được triển khai dưới dạng ma trận tam giác như trong Hình 2.2 (bên phải). Xây dựng EUCS rất nhanh (được thực hiện với một lần quét cơ sở dữ liệu) và chiếm một lượng bộ nhớ nhỏ, giới hạn bởi | I* | ´ | I*|, mặc dù trong thực tế, kích thước nhỏ hơn nhiều vì số lượng cặp hạn chế của các item cùng xảy ra trong các giao dịch. Sau khi xây dựng EUCS, việc khám phá tìm kiếm các mục đầu tiên bắt đầu bằng cách gọi thủ tục đệ quy Search với tập hợp mục rỗng ∅, tập hợp các mục đơn lẻ I*, minutil và cấu trúc EUCS.

Quy trình tìm kiếm (Thuật toán 2) lấy đầu vào một itemset P, phần mở rộng của P có dạng Pz có nghĩa là Pz đã được lấy trước đó bằng cách nối thêm một mục z vào P, minutil và cấu trúc EUCS. Thủ tục tìm kiếm hoạt động như sau. Đối với mỗi phần mở rộng Px của P, nếu tổng các giá trị iutil của utility-list của Px không nhỏ hơn minutil, thì Px là một itemset độ hữu ích cao và nó là đầu ra (xem tính chất 4).

Sau đó, nếu tổng giá trị iutils và rutils trong danh sách độ hữu ích của Px không nhỏ hơn minutil, thì các phần mở rộng của Px sẽ được tiếp tục khai thác. Điều này được thực hiện bằng cách hợp nhất Px với tất cả các phần mở rộng Py của P sao cho y ≻ x tạo thành các phần mở rộng có dạng Pxy có chứa | Px | + 1 items. Utility-list của Pxy sau đó được xây dựng như trong HUI-Miner bằng cách gọi thủ tục Construct (xem Thuật toán 3) để kết hợp danh sách độ hữu ích của P, Px và Py. Quy trình sau này giống như trong HUI-Miner và do đó không được nêu chi tiết ở đây. Sau đó, một cuộc gọi đệ quy đến thủ tục Search với Pxy được thực hiện để tính toán độ hữu ích của nó và khám phá độ hữu ích mở rộng của nó. Vì quy trình Search bắt đầu từ các mục đơn lẻ, nó khám phá đệ quy không gian tìm kiếm của các mục bằng cách nối thêm các mục đơn lẻ và nó chỉ cắt không gian tìm kiếm dựa trên tính chất 5. Có thể dễ dàng nhận thấy dựa trên tính chất 4 và 5 rằng quy trình này là chính xác và hoàn thành để khám phá tất cả các mục độ hữu ích cao.

Thuật toán 2. The Search procedure [6]

Dữ liệu đầu vào : một itemset P, phần mở rộng của P: một bộ các phần mở rộng của P, ngưỡng minutil, cấu trúc EUCS.

Dữ liệu đầu ra: bộ các itemset độ hữu ích cao.

1 Với mỗi itemset Px ∈ ExtensionsOfP thì thực hiện

2          if  SUM(Px.utilitylist.iutils) ≥ minutil then

3                       Dữ liệu đầu ra là Px;

4          end

5          if  SUM(Px.utilitylist.iutils)+SUM(Px.utilitylist.rutils) ≥ minutil thì

6                      ExtensionsOfPx ← ∅;

7                      Với mỗi itemset Py ∈ ExtensionsOfP phải đảm bảo y ≻ x thì thực hiện

8                                  if  ∃(x, y, c) ∈ EUCS sao cho c ≥ minutil) then

9                                              P xy ← P x ∪ P y;

10                                            P xy.utilitylist ← Construct (P, P x, P y);

11                                            ExtensionsOfPx ← ExtensionsOfPx ∪ P xy;

12                                end

13                    end

14                    Search (P x, ExtensionsOfPx, minutil);

15        end

16 end

Co-occurrence-based Pruning. Điểm mới chính trong FHM là một cơ chế cắt tỉa mới có tên EUCP (Estimated Utility Co-occurrence Pruning), dựa trên cấu trúc mới, EUCS (End User Computing Satisfaction). EUCP dựa trên thực nghiệm cho thấy rằng một trong những hoạt động tốn kém bộ nhớ nhất trong HUI-Miner là hoạt động kết hợp các item để tạo danh sách hữu ích cao. EUCP là một chiến lược cắt tỉa để loại bỏ trực tiếp phần mở rộng độ hữu ích thấp Pxy và tất cả các phần mở rộng bắc cầu của nó mà không xây dựng danh sách độ hữu ích của chúng. Điều này được thực hiện trên dòng 8 của quy trình Tìm kiếm. Điều kiện cắt tỉa là nếu không có bộ (x, y, c) trong EUCS sao cho c ≥ minutil, thì Pxy và tất cả các supersets( tập cha) của nó là các itemset độ hữu ích thấp và không cần phải khám phá.

Thuật toán 3. The Construct procedure [6]

Dữ liệu đầu vào: một itemset P, Px là mở rộng của P với một item x, Py: là mở rộng của P với một item y  

Dữ liệu đầu ra: Utility-list của Pxy

1 UtilityListOf Pxy ← ∅;

2 Với mỗi tuple ex ∈ Px.utilitylist thì thực hiện

3          if  ∃ey ∈ Py.utilitylist và ex.tid = exy.tid thì

4                      if  P.utilitylist = ∅ thì

5                                  Tìm kiếm phần tử e ∈ P.utilitylist sao cho e.tid = ex.tid.;

6                                  exy ← (ex.tid, ex.iutil + ey.iutil − e.iutil, ey.rutil);

7                      end

8                      else

9                                  exy ← (ex.tid, ex.iutil + ey.iutil, ey.rutil);

10                    end

11                    UtilityListOf Pxy ← UtilityListOf Pxy ∪ {exy};

12        end

13 end

14 return UtilityListPxy;

Chiến lược này là chính xác (chỉ cắt tỉa các mục độ hữu ích thấp). Bằng chứng là tính chất 3, nếu một itemset X chứa một itemset khác Y sao cho TWU (Y) < minutil, thì X và các siêu bộ của nó là các itemset độ hữu ích thấp.

Một câu hỏi quan trọng về chiến lược cắt tỉa EUCP là: chúng ta có nên không chỉ kiểm tra điều kiện đối với x,y trong mỗi lời gọi tới Search mà còn phải kiểm tra điều kiện đối với tất cả các cặp item duy nhất a,b thuộc Pxy ? Câu trả lời là không bởi vì thủ tục Search bị đệ quy do đó tất cả các cặp khác nhau của các item trong Pxy sẵn sàng được kiểm tra sau khi thủ Search được đệ quy tới Pxy.Ví dụ, hãy xem xét một mục Z = {a₁, a₂, a₃, a₄}. Để tạo ra itemset này, thủ tục Search đã kết hợp {a₁, a₂, a₃} và {a₁, a₂, a₄}, được tạo ra bởi {a₁, a₂} và {a₁, a₃} và {a₁, a₂} và {a₁ , a₄}, và chúng được tạo ra rừ các item đơn lẻ {a₁} {a₂} {a₃} {a₄}. Điều này có thể dễ dàng được thấ khi tạo ra Z, tất cả các cặp của các item trong Z đã được kiểm tra bởi EUCP ngoại trừ {a₃, a₄}.