TÌM KIẾM

TÌM KIẾM

Chương này giới thiệu bài toán tìm kiếm một phần tử trong một danh sách.
Phần trình bày tập trung chủ yếu vào hai giải thuật: tìm kiếm tuần tự và tìm kiếm nhị phân.

7.1. Giới thiệu
7.1.1. Khóa
Trong bài toán tìm kiếm, dựa vào một phần thông tin được gọi là khoá (key), chúng ta phải tìm một mẫu tin (record) chứa các thông tin khác liên quan với khoá này. Có thể có nhiều mẫu tin hoặc không có mẫu tin nào chứa khoá cần tìm.

                                           Hình 7.1. Mẫu tin và khoá.
7.1.2. Phân tích
 
 
 
Tìm kiếm thông thường là tác vụ tốn nhiều thời gian trong một chương trình. Vì thế việc tổ chức cấu trúc dữ liệu và giải thuật cho việc tìm kiếm có thể có những ảnh hưởng lớn đến hiệu suất hoạt động của chương trình. Ơ đây, thông số đo chủ yếu là số lần so sánh khoá cần tìm với các mẩu tin khác.

7.1.3. Tìm kiếm nội và tìm kiếm ngoại

Bài toán tìm kiếm bao gồm hai nhóm: tìm kiếm nội và tìm kiếm ngoại. Nếu lượng dữ liệu lớn phải lưu trên thiết bị lưu trữ ngoài như đĩa hay băng từ thì bài toán được gọi là tìm kiếm ngoại. Ngược lại nếu toàn bộ dữ liệu được lưu trữ trên bộ nhớ chính thì được gọi là tìm kiếm nội. Ơ đây ta quan tâm chủ yếu đến tìm kiếm nội.

Giải thuật tìm kiếm trên các cấu trúc liên kết hoàn toàn phụ thuộc vào cách tổ chức đặc trưng của chúng. Danh sách liên kết đơn là cấu trúc liên kết đơn giản nhất, việc tìm kiếm chỉ có thể duyệt tuần tự qua từng phần tử mà thôi. Đối với các cấu trúc liên kết khác, chúng ta sẽ có dịp tìm hiểu các chiến lược tìm kiếm khác nhau khi gặp từng cấu trúc cụ thể, chẳng hạn như cây nhị phân tìm kiếm, cây B-tree, hàng ưu tiên,…. Có một cấu trúc dữ liệu khá đặc biệt đối với việc tìm kiếm, đó là bảng băm. Ý tưởng cơ bản và đặc biệt nhất của bảng băm làm cho nó
 
khác với các cấu trúc dữ liệu khác ở chỗ, trong bảng băm không có khái niệm duyệt qua các phần tử trước khi đến được phần tử mong muốn. Chúng ta cũng sẽ được học về bảng băm trong chương 12.

Chương này chỉ trình bày những ý tưởng cơ bản và đơn giản nhất của việc tìm kiếm. Trong đó, giả sử rằng khi cần truy xuất một phần tử bất kỳ nào đó chúng ta có thể nhảy ngay đến vị trí của nó trong danh sách với thời gian là hằng số. Điều này chỉ có thể đạt được khi các phần tử được lưu trong danh sách liên tục. Và như vậy, trong chương này các giải thuật tìm kiếm rõ ràng chỉ phụ thuộc vào số lần so sánh khóa, chứ không phụ thuộc vào thời gian di chuyển qua các phần tử.

Cách hiện thực của các phương thức bổ sung cũng như các giải thuật tìm kiếm dưới đây hoàn toàn sử dụng các phương thức có sẵn của lớp List trong chương 4. Chúng ta nên có một số nhận xét như sau. Thứ nhất, cách sử dụng các phương thức có sẵn của lớp List không ngăn cấm chúng ta việc sử dụng hiện thực danh sách liên kết thay vì danh sách liên tục. Đối với danh sách liên kết cần phải chi phí trong khi truy xuất phần tử tại vị trí position nào đó (điều này vẫn còn điểm khác nhau giữa hai phương án của danh sách liên kết có hoặc không có lưu lại thuộc tính current_position). Đối với danh sách liên tục, có thể trực tiếp truy xuất một phần tử thông qua một số nguyên chỉ vị trí của nó, thay vì gọi phương thức có sẵn retrieve.

7.1.4. Lớp Record và lớp Key

Chúng ta có một số quy ước như sau. Các phần tử trong danh sách đang được tìm kiếm thoả các tiêu chuẩn tối thiểu sau:
•    Mỗi mẫu tin có một khoá đi kèm.
•    Các khóa có thể được so sánh với nhau bằng các toán tử so sánh.
•    Một mẩu tin có thể được chuyển đổi tự động thành một khóa. Do đó có thể so sánh các mẫu tin với nhau hoặc so sánh mẫu tin với khoá thông qua việc việc chuyển đổi mẫu tin về khóa liên quan đến nó.

Chúng ta sẽ cài đặt các chương trình tìm kiếm làm việc với các đối tượng thuộc lớp Record thoả các điều kiện trên. Ngoài ra còn có một lớp Key (có thể trùng với Record) và một tác vụ để chuyển đổi một Record thành một Key. Tác vụ đó có thể được cài đặt theo một trong hai cách sau:
•    Một phương thức của lớp Record có khai báo là operator Key() const;
•    Một constructor của lớp Key có khai báo là Key(const Record&);

Nếu Record và Key là giống nhau thì không cần tác vụ này.
 
Trên lớp Key chúng ta cần phải định nghĩa các phép so sánh ==, !=, <, >,
<=, >= mọi cặp đối tượng thuộc lớp Key. Do mọi Record đều có thể được chuyển
đổi thành Key nhờ trình biên dịch bằng một trong các tác vụ trên, các tác vụ so sánh Key đều có thể được sử dụng để so sánh hai Record hay so sánh một Record với một Key.

// Khai báo cho lớp Key class Key{
public:
//    Các constructor và các phương thức.
private:
//    Các thuộc tính của Key.
};

//    Khai báo các tác vụ so sánh cho khoá.
bool operator ==(const Key &x, const Key &y);
bool operator > (const Key &x, const Key &y); bool operator < (const Key &x, const Key &y); bool operator >=(const Key &x, const Key &y); bool operator <=(const Key &x, const Key &y); bool operator !=(const Key &x, const Key &y);

// Khai báo cho lớp Record class Record{
public:
operator Key(); //    Chuyển đổi từ Record sang Key.
//    Các constructor và các phương thức của Record. private:
//  Các thuộc tính của Record
};

7.1.5. Thông số

Các hàm tìm kiếm sẽ nhận hai tham trị. Tham trị thứ nhất là danh sách cần tìm, tham trị thứ hai là phần tử cần tìm. Thông số thứ hai được gọi là đích của phép tìm kiếm. Trị trả về của hàm có kiểu là ErrorCode cho biết việc tìm kiếm có thành công hay không. Nếu tìm thấy thì tham biến position chứa vị trí tìm thấy phần tử liên quan đến khóa cần tìm trong danh sách.

7.2. Tìm kiếm tuần tự

7.2.1. Giải thuật và hàm

Phương pháp đơn giản nhất để tìm kiếm là xuất phát từ một đầu của danh sách và tìm dọc theo danh sách cho đến khi gặp được phần tử cần tìm hay đến khi hết danh sách. Đây là giải thuật được sử dụng trong hàm sau.
 
ErrorCode sequential_search(const List<Record> &the_list,
const Key &target, int &position)
/*
post: Nếu có phần tử trong danh sách có khóa trùng với target, hàm trả về success và tham biến position chứa vị trí của phần tử được tìm thấy trongt danh sách. Ngược lại hàm trả về not_present và position không có nghĩa.
*/
{
int s = the_list.size();
for (position = 0; position < s; position++) {
Record data; the_list.retrieve(position, data); if (data == target) return success;
}
return not_present;
}

Vòng lặp for trong hàm này duyệt danh sách cho đến khi gặp phần tử cần
tìm hoặc đến khi hết danh sách. Nếu gặp phần tử cần tìm thì giải thuật kết thúc
ngay lập tức và position chứa vị trí phần tử tìm được, ngược lại nếu không tìm thấy thì hàm trả về not_present và position chứ vị trí không hợp lệ.

7.2.2. Phân tích

Sau đây chúng ta sẽ đánh giá khối lượng công việc mà giải thuật tìm kiếm tuần tự thực hiện để làm cơ sở so sánh với các phương pháp khác sau này.

Giả sử giải thuật tìm kiếm tuần tự được thực thi trên một danh sách dài. Các lệnh ngoài vòng for được thực hiện một lần, do đó không ảnh hưởng nhiều đến thời gian chạy giải thuật. Trong mỗi lần lặp, một khoá của một mẫu tin được so sánh với khoá đích. Ngoài ra còn có một số tác vụ khác cũng được thực hiện một lần cho mỗi lần lặp.

Như vậy các tác vụ mà ta cần quan tâm có liên hệ trực tiếp với số lần so sánh khoá. Những cách lập trình khác nhau của cùng một giải thuật có thể cho ra các số lượng công việc khác nhau nhưng đều cho cùng một số lần so sánh. Khi chiều dài của danh sách thay đổi thì số lượng công việc cũng thay đổi theo một cách tương ứng.

Ơ đây chúng ta sẽ tìm hiểu sự phụ thuộc của số lần so sánh khoá vào độ dài của danh sách. Đây là thông tin hữu ích nhất trong việc tìm hiểu giải thuật tìm kiếm này, nó không phụ thuộc vào cách thức lập trình cụ thể cũng như loại máy tính cụ thể đang được sử dụng. Việc phân tích các giải thuật tìm kiếm được dựa trên giả thiết căn bản là: khối lượng công việc mà một giải thuật tìm kiếm thực hiện (hay thời gian chạy của giải thuật) được phản ảnh bởi tổng số lần so sánh khoá mà giải thuật thực hiện.
 
Chúng ta hãy tìm số lần so sánh khoá mà giải thuật tìm kiếm tuần tự cần khi nó chạy trên một danh sách gồm n phần tử. Do giải thuật tìm kiếm tuần tự lần lượt so sánh khoá đích với từng khoá của các phần tử trong danh sách nên tổng số lần so sánh phụ thuộc vào vị trí của đích trong danh sách. Nếu đích là phần tử đầu tiên của danh sách thì chỉ cần một lần so sánh. Nếu đích là phần tử cuối cùng của danh sách thì cần n lần so sánh. Nếu phép tìm kiếm không thành công (không có phần tử  đích trong danh sách) thì số lần so sánh cũng là n. Như vậy, trong trường hợp tốt nhất, giải thuật tìm kiếm tuần tự chỉ cần một lần so sánh, còn trong trường hợp xấu nhất thì nó cần n lần so sánh.

Trong phần lớn các trường hợp, chúng ta không biết chính xác đặc điểm của các danh sách cần tìm kiếm, do đó chúng ta thường không áp dụng được các kết quả về thời gian chạy “tốt nhất” và “xấu nhất” trên kia. Trong các trường hợp này, chúng ta thường sử dụng thời gian chạy trung bình. Ơ đây trung bình có nghĩa là chúng ta xét mỗi khả năng một lần và lấy kết quả trung bình của chúng. Tức là chúng ta giả sử các trường hợp cần tìm xảy ra với xác suất như nhau. Lưu ý rằng trong thực tế không phải lúc nào giả thiết này cũng phù hợp.

Chúng ta có số lần so sánh trung bình của giải thuật tìm kiếm tuần tự (trường hợp thành công) như sau.
1 + 2 + 3 + ... + n = 1 (n + 1)
n    2

7.3. Tìm kiếm nhị phân

Giải thuật tìm kiếm tuần tự có thể được cài đặt dễ dàng và khá hiệu quả với những danh sách ngắn nhưng với những danh sách dài thì giải thuật chạy rất chậm. Với các danh sách dài, có nhiều phương pháp hữu hiệu hơn để giải quyết bài toán tìm kiếm, nhưng với điều kiện là các khoá của danh sách đã được sắp xếp sẵn.

Một trong những phương pháp tốt nhất để tìm kiếm trên một danh sách mà các khoá đã được sắp xếp là tìm kiếm nhị phân. Trong phương pháp này, chúng ta so sánh khoá đích với khoá của phần tử ở giữa của danh sách. Tuỳ thuộc vào khoá đích nằm trước hay sau khoá ở giữa mà chúng ta tiếp tục quá trình tìm kiếm trong nửa đầu hay nửa sau của danh sách. Với cách này, tại mỗi bước chúng ta giảm kích thước của danh sách cần tìm đi một nửa. Một danh sách chứa khoảng một triệu phần tử sẽ được xử lý trong khoảng hai mươi lần so sánh.
 
7.3.1. Danh sách có thứ tự

Sau đây chúng ta định nghĩa một kiểu dữ liệu trừu tượng cho một danh sách có thứ tự.

Định nghĩa: Danh sách có thứ tự (ordered list) là danh sách trong đó mỗi phần tử có chứa một khoá sao cho các khoá này đã được sắp thứ tự. Tức là nếu phần tử i đứng trước phần tử j trong danh sách thì khoá của i nhỏ hơn hay bằng khoá của j.

Để tìm kiếm nhị phân, danh sách cần phải có thứ tự. Chúng ta cài đặt danh
sách có thứ tự là một lớp được thừa kế từ lớp List đã có và viết lại các phương thức insert và replace.

class Ordered_list:public List<Record>{
public: Ordered_list();
ErrorCode insert(const Record &data);
ErrorCode replace(int position, const Record &data);
};

Phương thức insert trên chèn một phần tử vào đúng vị trí của nó trong danh
sách dựa vào thứ tự của các khoá. Nếu danh sách chứa nhiều khoá trùng với khoá của phần tử đang thêm vào thì khoá mới sẽ là phần tử đầu tiên trong số các phần tử có khoá trùng nhau.

ErrorCode Ordered_list::insert(const Record &data)
/*
post: Nếu danh sách chưa đầy, phần tử mới data được chèn vào vị trí ngay sau phần tử lớn
nhất trong số các phần tử nhỏ hơn nó, phương thức trả về success, ngược lại phương thức trả về overflow.
*/
{
int s = size();
int position;
for (position = 0; position < s; position++) { // Tìm vị trí thích hợp.
Record list_data;
retrieve(position, list_data);
if (data >= list_data) break;
}
return insert(position, data); // Gọi phương thức đã có của lớp List.
}

Phương thức replace cũng cần kiểm tra tính hợp lệ của phần tử được thay
thế sao cho danh sách vẫn đảm bảo thứ tự.
 
7.3.2. Xây dựng giải thuật

Để đảm bảo rằng giải thuật được xây dựng sẽ cho ra kết quả đúng đắn, chúng ta cần mô tả rõ ràng về ý nghĩa của các biến sử dụng trong chương trình và các điều kiện cần phải thoả trước và sau mỗi vòng lặp, đồng thời vòng lặp cũng phải được đảm bảo rằng sẽ dừng đúng.

Giải thuật tìm kiếm nhị phân sẽ sử dụng hai chỉ số, top và bottom, để giới hạn phần danh sách mà chúng ta đang tiến hành tìm kiếm. Tại mỗi bước, giải thuật giảm kích thước của phần này đi khoảng một nửa. Để tiện theo dõi tiến trình của giải thuật, chúng ta cần xác nhận một điều rằng, trước mỗi lần lặp có một điều kiện luôn đúng: khoá đích, nếu có trong danh sách, phải luôn nằm trong khoảng từ bottom đến top, có kể cả hai vị trí này. Điều kiện này lúc đầu được bảo đảm bằng cách đặt bottom bằng 0 và top là the_list.size()–1.

Trước tiên , giải thuật tìm vị trí phần tử ở giữa bottom và top theo công thức

mid =
 
(bottom + top)

2
 
Kế đó giải thuật so sánh khoá đích với khoá của phần tử tại vị trí mid và thay đổi top hoặc bottom dựa theo kết quả của phép so sánh này.

Chúng ta lưu ý rằng giải thuật nên kết thúc khi top ≤  bottom; tức là khi phần danh sách cần tìm còn không quá một phần tử (giả sử rằng giải thuật đã không chấm dứt sớm hơn trước đó trong trường hợp khoá đích đã được tìm thấy).

Cuối cùng, để chắc chắn rằng giải thuật dừng, số phần tử cần tìm của danh sách (top – bottom + 1) phải giảm sau mỗi lần lặp của giải thuật.

7.3.3. Phiên bản thứ nhất

Cách cài đặt đơn giản nhất của giải thuật là cứ tiếp tục chia đôi danh sách, bất kể khoá đích có được tìm thấy hay chưa, cho tới khi danh sách còn lại có chiều dài là 1.
Hàm sau đây được viết đệ qui.

Error_code recursive_binary_1(const Ordered_list &the_list, const Key
&target, int bottom, int top, int &position)
/*
pre:    Các chỉ số bottom và top chỉ ra dãy các phần tử trong danh sách phục vụ cho việc tìm kiếm target.
post: Nếu phần tử có khóa trùng với target được tìm thấy thì trả về success, position chỉ vị trí tìm thấy. Ngược lại phương thức trả về not_present, position không có nghĩa.
uses: recursive_binary_1 và các phương thức của lớp List và Record.
 
*/
{
Record data;
if (bottom < top) {    // List có nhiều hơn 1 phần tử.
int mid = (bottom + top) / 2;
the_list.retrieve(mid, data);
if (data < target)    // Cần loại bỏ một nửa số phần tử bên phải.
return recursive_binary_1(the_list, target, mid + 1, top, position);
else    // Cần loại bỏ một nửa số phần tử bên trái.
return recursive_binary_1(the_list, target, bottom, mid, position);
}
else if (top < bottom)
return not_present;    // List rỗng.
else {    // List có chính xác 1 phần tử.
position = bottom;
the_list.retrieve(bottom, data);
if (data == target) return success;
else return not_present;
}
}

Sự phân chia của danh sách trong quá trình tìm kiếm có thể được minh hoạ
như sau:

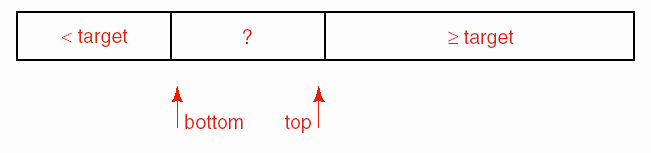
Lưu ý rằng trong sơ đồ này phần đầu tiên chỉ chứa các phần tử nhỏ hơn khoá đích còn phần cuối có thể chứa các phần tử lớn hơn hoặc bằng khoá đích. Bằng cách này, khi phần giữa của danh sách chỉ còn một phần tử mà lại là phần tử chứa khóa đích thì phần tử này luôn là phần tử đầu tiên nếu có nhiều phần tử có khoá trùng với nó trong danh sách.

Nếu danh sách là rỗng thì hàm trên thất bại, ngược lại nó tính giá trị của mid. Vì mid được tính là trung bình của top và bottom nên nó nằm giữa top và bottom, và do đó nó là chỉ số hợp lệ của một phần tử của danh sách.

Biểu thức chia nguyên luôn làm tròn xuống, nên chúng ta có

bottom ≤    mid < top

Sau khi quá trình đệ qui kết thúc, giải thuật phải kiểm tra xem khoá đích đã được tìm thấy hay chưa vì quá trình đệ qui không thực hiện phép kiểm tra này.

Để chuyển hàm trên về dạng hàm tìm kiếm chuẩn mà chúng ta định ra ở trên chúng ta định nghĩa hàm sau:
 
Error_code run_recursive_binary_1(const Ordered_list &the_list, const Key &target, int &position)
{
return recursive_binary_1(the_list, target, 0, the_list.size() - 1,
position);
}

Vì phép đệ qui được sử dụng trong hàm trên là đệ qui đuôi (tail recursion) nên có thể chuyển thành vòng lặp một cách dễ dàng. Đồng thời chúng ta có thể làm
cho các thông số của hàm trở nên thống nhất với các hàm tìm kiếm khác.

ErrorCode binary_search_1 (const Ordered_list &the_list,
const Key &target, int &position)
/*
post: Nếu phần tử có khóa trùng với target được tìm thấy thì trả về success, position chỉ vị trí tìm thấy. Ngược lại phương thức trả về not_present, position không có nghĩa.
uses: Các phương thức của lớp List và Record.
*/
{
Record data;
int bottom = 0, top = the_list.size() - 1;

while (bottom < top) {
int mid = (bottom + top) / 2; the_list.retrieve(mid, data); if (data < target)
bottom = mid + 1;
else
top = mid;
}
if (top < bottom) return not_present;
else {
position = bottom;
the_list.retrieve(bottom, data);
if (data == target) return success;
else return not_present;
}
}

7.3.4. Nhận biết sớm phần tử có chứa khóa đích

Tuy binary_search_1 là một dạng đơn giản của giải thuật tìm kiếm nhị phân, nhưng nó thực hiện thừa một số lần so sánh vì nó không nhận ra trường hợp phần tử khoá được tìm thấy sớm hơn. Vì thế chúng ta có thể cải tiến giải thuật như sau.

Error_code recursive_binary_2(const Ordered_list &the_list, const Key
&target,int bottom, int top, int &position)
/*
pre:    Các chỉ số bottom và top chỉ ra dãy các phần tử trong danh sách phục vụ cho việc tìm kiếm target.
 
post: Nếu phần tử có khóa trùng với target được tìm thấy thì trả về success, position chỉ vị trí tìm thấy. Ngược lại phương thức trả về not_present, position không có nghĩa.
uses: recursive_binary_2 và các phương thức của lớp List và Record.
*/
{
Record data;
if (bottom <= top) {
int mid = (bottom + top) / 2;
the_list.retrieve(mid, data);
if (data == target) { position = mid; return success;
}

else if (data < target)
return recursive_binary_2(the_list, target, mid + 1, top, position);
else
return recursive_binary_2(the_list, target, bottom, mid - 1,
position);
}
else return not_present;
}

Error_code run_recursive_binary_2(const Ordered_list &the_list, const Key &target, int &position)
{
return recursive_binary_2(the_list, target, 0, the_list.size() - 1,
position);
}

Chúng ta có thể chuyển hàm này thành dạng không đệ qui như sau.

Error_code binary_search_2(const Ordered_list &the_list, const Key &target, int &position)
/*
post: Nếu phần tử có khóa trùng với target được tìm thấy thì trả về success, position chỉ vị trí tìm thấy. Ngược lại phương thức trả về not_present, position không có nghĩa.
uses: Các phương thức của lớp List và Record.
*/
{
Record data;
int bottom = 0, top = the_list.size() - 1;
while (bottom <= top) {
position = (bottom + top) / 2; the_list.retrieve(position, data); if (data == target) return success;
if (data < target) bottom = position + 1;
else top = position - 1;
}
return not_present;
}

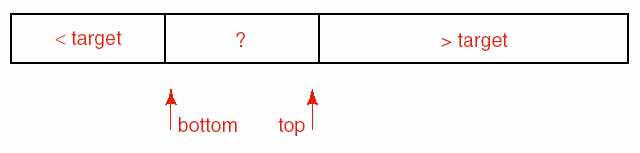
Các hoạt động này có thể được minh họạ như sau:
 

 
Sơ đồ này là đối xứng theo nghĩa phần thứ nhất chỉ chứa các phần tử nhỏ hơn khoá, phần thứ ba chỉ chứa các phần tử lớn hơn khoá. Khi đó, nếu như khoá xuất
hiện ở nhiều vị trí trong danh sách thì giải thuật có thể trả về bất kỳ vị trí nào trong số đó. Đây cũng là nhược điểm của cách cải tiến để nhận ra sớm phần tử cần tìm này, vì trong một số ứng dụng, vị trí tương đối giữa phần tử được tìm
thấy so với các phần tử có khóa trùng với nó rất quan trọng.

7.4. Cây so sánh

Cây so sánh (comparison tree) của một giải thuật tìm kiếm, còn gọi là cây quyết định (decision tree) hay cây tìm kiếm (search tree), là một cây có được bằng cách lần theo vết các hành vi của giải thuật. Mỗi nút của cây biểu diễn một phép so sánh. Tên của nút là chỉ số của phần tử có khóa đang được so sánh với khóa đích. Các nhánh xuất phát từ  mỗi nút là các kết quả có thể có của phép so sánh tại nút đó và được đặt tên tương ứng. Khi giải thuật kết thúc chúng ta có một nút lá. Nếu giải thuật thất bại thì nút lá này được đặt tên là F, ngược lại tên của nút là chỉ số của phần tử có khoá trùng với khoá đích.

Cây so sánh cho giải thuật tìm kiếm tuần tự rất đơn giản:

Hình 7.2- Cây so sánh cho tìm kiếm tuần tự

Số lần so sánh mà một giải thuật tìm kiếm thực hiện khi tiến hành một phép tìm kiếm cụ thể là số nút trung gian mà giải thuật đi qua kể từ gốc (nút trên cùng của cây) để đi đến nút lá cần thiết.
 
Hình dạng của cây so sánh cho tìm kiếm nhị phân:

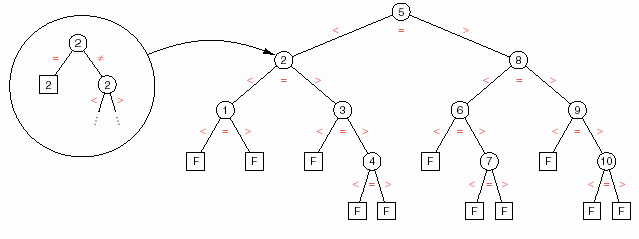
Giải thuật tìm kiếm tuần tự cần nhiều phép so sánh hơn giải thuật tìm kiếm nhị phân. Chúng ta dễ dàng nhận thấy điều này qua hình dạng các cây so sánh của chúng. Giải thuật tìm kiếm tuần tự có cây so sánh hẹp và cao trong khi cây so sánh của giải thuật tìm kiếm nhị phân rộng và thấp hơn nhiều. Hình dạng cây này giúp ta hiểu được tại sao số lần so sánh trong phép tìm kiếm nhị phân là ít hơn so với tìm kiếm tuần tự.

Hình 7.3- Cây so sánh cho tìm kiếm nhị phân.