Chương 8 – SẮP XẾP
Chương này giới thiệu một số phương pháp sắp xếp cho cả danh sách liên tục
và danh sách liên kết.
8.1. Giới thiệu
Để truy xuất thông tin nhanh chóng và chính xác, người ta thường sắp xếp thông tin theo một trật tự hợp lý nào đó. Có một số cấu trúc dữ liệu mà định nghĩa của chúng đã bao hàm trật tự của các phần tử, khi đó mỗi phần tử khi thêm vào đều phải đảm bảo trật tự này. Trong chương này chúng ta sẽ tìm hiểu việc sắp xếp các danh sách chưa có thứ tự trở nên có thứ tự.
Vì sắp xếp có vai trò quan trọng nên có rất nhiều phương pháp được đưa ra để giải quyết bài toán này. Các phương pháp này khác nhau ở nhiều điểm, trong đó điểm quan trọng nhất là dữ liệu cần sắp xếp nằm toàn bộ trong bộ nhớ chính (tương ứng các giải thuật sắp xếp nội) hay có một phần nằm trong thiết bị lưu trữ ngoài (tương ứng các giải thuật sắp xếp ngoại). Trong chương này chúng ta chỉ xem xét một số giải thuật sắp xếp nội.
Chúng ta sẽ sử dụng các lớp đã có ở chương 4 và chương 7. Ngoài ra, trong trường hợp khi có nhiều phần tử khác nhau có cùng khóa thì các giải thuật sắp xếp khác nhau sẽ cho ra những thứ tự khác nhau giữa chúng, và đôi khi sự khác nhau này cũng có ảnh hưởng đến các ứng dụng.
Trong các giải thuật tìm kiếm, khối lượng công việc phải thực hiện có liên quan chặt chẽ với số lần so sánh các khóa. Trong các giải thuật sắp xếp thì điều này cũng đúng. Ngoài ra, các giải thuật sắp xếp còn phải di chuyển các phần tử. Công việc này cũng chiếm nhiều thời gian, đặc biệt khi các phần tử có kích thước lớn được lưu trữ trong danh sách liên tục.
Để có thể đạt được hiệu quả cao, các giải thuật sắp xếp thường phải tận dụng các đặc điểm riêng của từng loại cấu trúc dữ liệu. Chúng ta sẽ viết các giải thuật sắp xếp dưới dạng các phương thức của lớp List.
template <class Record>
class Sortable_list:public List<Record> {
public: // Khai báo của các phương thức sắp xếp được thêm vào đây
private: // Các hàm phụ trợ.
};
Chúng ta có thể sử dụng bất kỳ dạng hiện thực nào của lớp List trong chương
4. Các phần tử dữ liệu trong Sortable_list có kiểu là Record. Như đã giới
thiệu trong chương 7, Record có các tính chất sau đây:
• Mỗi mẫu tin có một khoá đi kèm.
• Các khóa có thể được so sánh với nhau bằng các toán tử so sánh.
• Một mẩu tin có thể được chuyển đổi tự động thành một khóa. Do đó có thể so sánh các mẫu tin với nhau hoặc so sánh mẫu tin với khoá thông qua việc chuyển đổi mẫu tin về khóa liên quan đến nó.
8.2. Sắp xếp kiểu chèn (Insertion Sort)
Phương pháp sắp xếp chen vào dựa trên ý tưởng chèn phần tử vào danh sách đã có thứ tự.
8.2.1. Chèn phần tử vào danh sách đã có thứ tự
Định nghĩa danh sách có thứ tự đã được trình bày trong chương 7.
Với các danh sách có thứ tự, một số tác vụ chỉ sử dụng khóa của phần tử chứ không sử dụng vị trí của phần tử:
• retrieve: truy xuất một phần tử có khóa cho trước.
• insert: chèn một phần tử có khóa cho trước sao cho danh sách vẫn còn thứ tự, vị trí của phần tử mới được xác định bởi khóa của nó.
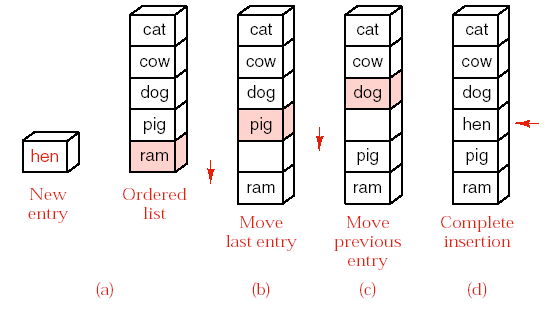
Hình 8.1 – Chèn phần tử vào danh sách đã có thứ tự.
Phép thêm vào và phép truy xuất có thể không cho kết quả duy nhất trong
trường hợp có nhiều phần tử trùng khóa. Phép truy xuất phần tử dựa trên khóa chính là phép tìm kiếm đã được trình bày trong chương 7.
Để thêm phần tử mới vào danh sách liên tục đã có thứ tự, các phần tử sẽ đứng sau nó phải được dịch chuyển để tạo chỗ trống. Chúng ta cần thực hiện phép
tìm kiếm để tìm vị trí chen vào. Vì danh sách đã có thứ tự nên ta có thể sử dụng phép tìm kiếm nhị phân. Tuy nhiên, do thời gian cần cho việc di chuyển các phần tử lớn hơn nhiều so với thời gian tìm kiếm, nên việc tiết kiệm thời gian tìm kiếm cũng không cải thiện thời gian chạy toàn bộ giải thuật được bao nhiêu. Nếu việc tìm kiếm tuần tự từ cuối danh sách có thứ tự được thực hiện đồng thời với việc di chuyển phần tử, thì chi phí cho một lần chen một phần tử mới là tối thiểu.
8.2.2. Sắp xếp kiểu chèn cho danh sách liên tục
Tác vụ thêm một phần tử vào danh sách có thứ tự là cơ sở của phép sắp xếp kiểu chèn. Để sắp xếp một danh sách chưa có thứ tự, chúng ta lần lượt lấy ra từng phần tử của nó và dùng tác vụ trên để đưa vào một danh sách lúc đầu là rỗng.
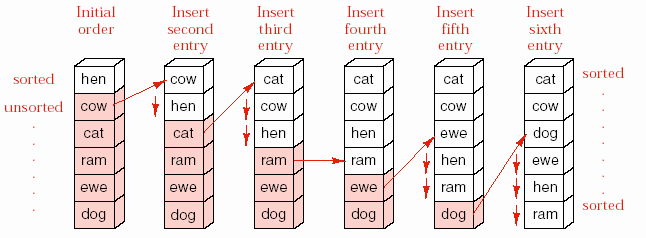
Hình 8.2- Ví dụ về sắp xếp kiểu chèn cho danh sách liên tục.
Phương pháp này được minh họa trong hình 8.2. Hình này chỉ ra các bước cần
thiết để sắp xếp một danh sách có 6 từ. Nhìn hình vẽ chúng ta thấy, phần danh sách đã có thứ tự gồm các phần tử từ chỉ số sorted trở lên trên, các phần tử từ
chỉ số unsorted trở xuống dưới là chưa có thứ tự. Bước đầu tiên, từ “hen” được xem là đã có thứ tự do danh sách có một phần tử đương nhiên là danh sách có thứ tự. Tại mỗi bước, phần tử đầu tiên trong phần danh sách bên dưới được lấy ra và chèn vào vị trí thích hợp trong phần danh sách đã có thứ tự bên trên. Để có chỗ chèn phần tử này, một số phần tử khác trong phần danh sách đã có thứ tự được di chuyển về phía cuối danh sách.
Trong phương thức duới đây, first_unsorted là chỉ số phần tử đầu tiên trong phần danh sách chưa có thứ tự, và current là biến tạm nắm giữ phần tử này cho đến khi tìm được chỗ trống để chèn vào.
Hình 8.3- Bước chính của giải thuật sắp xếp kiểu chèn.
// Dành cho danh sách liên tục trong chương 4.
template <class Record>
void Sortable_list<Record>::insertion_sort()
/*
post: Các phần tử trong danh sách đã được sắp xếp theo thứ tự không giảm.
uses: Các phương thức của lớp Record.
*/
{
int first_unsorted;//Chỉ số phần tử đầu tiên trong phần danh sách chưa có thứ tự.
int position; // Chỉ số dùng cho việc di chuyển các phần tử về phía sau.
Record current;// Nắm giữ phần tử đang được tìm chỗ chèn vào phần danh sách đã có thứ tự.
for (first_unsorted = 1; first_unsorted < count; first_unsorted++)
if (entry[first_unsorted] < entry[first_unsorted - 1]) {
position = first_unsorted;
current = entry[first_unsorted];
do { // Di chuyển dần các phần tử về phía sau để tìm chỗ trống thích hợp.
entry[position] = entry[position - 1];
position--;
} while (position > 0 && entry[position - 1] > current);
entry[position] = current;
}
}
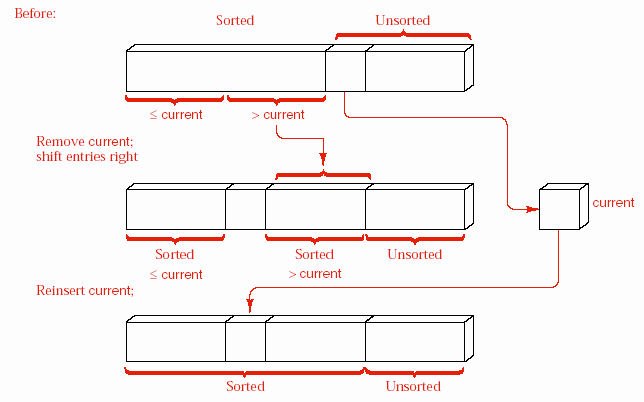
Vì danh sách có một phần tử xem như đã có thứ tự nên vòng lặp trên biến first_unsorted bắt đầu với phần tử thứ hai. Nếu phần tử này đã ở đúng vị trí thì không cần phải tiến hành thao tác nào. Ngược lại, phần tử được đưa vào biến current, vòng lặp do...while đẩy các phần tử lùi về sau một vị trí cho đến khi tìm được vị trí đúng cho current. Trường hợp vị trí đúng của current là đầu dãy cần được nhận biết riêng bởi điều kiện thoát khỏi vòng lặp là position==0.
8.2.3. Sắp xếp kiểu chèn cho danh sách liên kết
Với danh sách liên kết, chúng ta không cần di chuyển các phần tử, do đó cũng không cần bắt đầu tìm kiếm từ phần tử cuối của phần danh sách đã có thứ tự. Hình 8.4 minh họa giải thuật này. Con trỏ last_sorted chỉ phần tử cuối cùng của phần danh sách đã có thứ tự, last_sorted->next chỉ phần tử đầu tiên của phần danh sách chưa có thứ tự. Ta dùng biến first_unsorted để chỉ vào phần tử này và biến current để tìm vị trí thích hợp cho việc chèn phần tử
*first_unsorted vào. Nếu vị trí đúng của *first_unsorted là đầu danh sách thì nó được chèn vào vị trí này. Ngược lại, current được di chuyển về phía cuối danh sách cho đến khi có (current->entry >= first_unsorted->entry) và
*first_unsorted được thêm vào ngay trước *current. Để có thể thực hiện việc thêm vào trước current, chúng ta cần một con trỏ trailing luôn đứng trước current một vị trí.
Hình 8.4- Sắp xếp kiểu chèn cho danh sách liên kết.
Như chúng ta đã biết, phần tử cầm canh (sentinel) là một phần tử được thêm vào một đầu của danh sách để đảm bảo rằng vòng lặp luôn kết thúc mà không cần phải thực hiện bổ sung một phép kiểm tra nào. Vì chúng ta đã có
last_sorted->next == first_unsorted,
nên phần tử *first_unsorted đóng luôn vai trò của phần tử cầm canh trong khi current tiến dần về phía cuối phần danh sách đã có thứ tự. Nhờ đó, điều kiện dừng của vòng lặp di chuyển current luôn được đảm bảo.
Ngoài ra, danh sách rỗng hay danh sách có một phần tử là đương nhiên có thứ tự, nên ta có thể kiểm tra trước dễ dàng.
Mặc dù cơ chế hiện thực của sắp xếp kiểu chèn cho danh sách liên kết và cho danh sách liên tục có nhiều điểm khác nhau nhưng về ý tưởng thì hai phiên bản này rất giống nhau. Điểm khác biệt lớn nhất là trong danh sách liên kết việc tìm kiếm được thực hiện từ đầu danh sách trong khi trong danh sách liên tục việc tìm kiếm được thực hiện theo chiều ngược lại.
// Dành cho danh sách liên kết trong chương 4.
template <class Record>
void Sortable_list<Record>::insertion_sort()
/*
post: Các phần tử trong danh sách đã được sắp xếp theo thứ tự không giảm.
uses: Các phương thức của lớp Record.
*/
{
Node <Record> *first_unsorted,
*last_sorted,
*current,
*trailing;
|
if (head != NULL) {
|
|
// Loại trường hợp danh sách rỗng và
|
|
last_sorted =
|
head;
|
// trường hợp danh sách chỉ có 1 phần tử.
|
while (last_sorted->next != NULL) {
first_unsorted = last_sorted->next;
if (first_unsorted->entry < head->entry) {
// *first_unsorted được chèn vào đầu danh sách. last_sorted->next = first_unsorted->next; first_unsorted->next = head;
head = first_unsorted;
}
else {
// Tìm vị trí thích hợp.
trailing = head;
current = trailing->next;
while (first_unsorted->entry > current->entry) {
trailing = current;
current = trailing->next;
}
// *first_unsorted được chèn vào giữa *trailing và *current.
if (first_unsorted == current)
last_sorted = first_unsorted; // vị trí đang có đã đúng.
else {
last_sorted->next = first_unsorted->next;
first_unsorted->next = current;
trailing->next = first_unsorted;
}
}
}
}
}
Thời gian cần thiết để sắp xếp danh sách dùng giải thuật sắp xếp kiểu chèn tỉ
lệ với bình phương số phần tử của danh sách.
8.3. Sắp xếp kiểu chọn (Selection Sort)
Sắp xếp kiểu chèn có một nhược điểm lớn. Sau khi một số phần tử đã được sắp xếp vào phần đầu của danh sách, việc sắp xếp một phần tử phía sau đôi khi đòi hỏi phải di chuyển phần lớn các phần tử đã có thứ tự này. Mỗi lần di chuyển, các phần tử chỉ được di chuyển một vị trí, do đó nếu một phần tử cần di chuyển 20 vị trí để đến được vị trí đúng cuối cùng của nó thì nó cần được di chuyển 20 lần. Nếu kích thước của mỗi phần tử là nhỏ hoặc chúng ta sử dụng danh sách liên kết thì việc di chuyển này không cần nhiều thời gian lắm. Nhưng nếu kích thước mỗi phần tử lớn và danh sách là liên tục thì thời gian di chuyển các phần tử sẽ rất lớn. Như vậy, nếu như mỗi phần tử, khi cần phải di chuyển, được di chuyển ngay đến vị trí đúng sau cùng của nó thì giải thuật sẽ chạy hiệu quả hơn nhiều. Sau đây chúng ta trình bày một giải thuật để đạt được điều đó.
8.3.1. Giải thuật
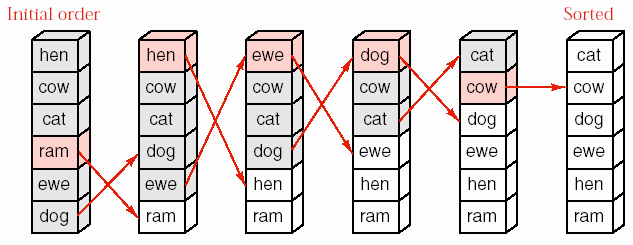
Hình 8.5- Ví dụ sắp xếp kiểu chọn.
Hình 8.5 trình bày một ví dụ sắp xếp 6 từ theo thứ tự của bảng chữ cái. Tại bước đầu tiên, chúng ta tìm phần tử sẽ đứng tại vị trí cuối cùng trong danh sách có thứ tự và tráo đổi vị trí với phần tử cuối cùng hiện tại. Trong các bước kế tiếp, chúng ta tiếp tục lặp lại công việc trên với phần còn lại của danh sách không kể các phần tử đã được chọn trong các bước trước. Khi phần danh sách chưa được sắp xếp chỉ còn lại một phần tử thì giải thuật kết thúc.
Bước tổng quát trong sắp xếp kiểu chọn được minh họa trong hình 8.6. Các phần tử có khóa lớn đã được sắp theo thứ tự và đặt ở phần cuối danh sách. Các phần tử có khóa nhỏ hơn chưa được sắp xếp. Chúng ta tìm trong số những phần tử chưa được sắp xếp để lấy ra phần tử có khóa lớn nhất và đổi chỗ nó về cuối các phần tử này. Bằng cách này, tại mỗi bước, một phần tử được đưa về đúng vị trí cuối cùng của nó.
Hình 8.6- Một bước trong sắp xếp kiểu chọn.
8.3.2. Sắp xếp chọn trên danh sách liên tục
Sắp xếp chọn giảm tối đa việc di chuyển dữ liệu do mỗi bước đều có ít nhất một phần tử được đặt vào đúng vị trí cuối cùng của nó. Vì vậy sắp xếp kiểu chọn thích hợp cho các danh sách liên tục có các phần tử có kích thước lớn. Nếu các phần tử có kích thước nhỏ hay danh sách có hiện thực là liên kết thì sắp xếp kiểu chèn thường nhanh hơn sắp xếp kiểu chọn. Do đó chúng ta chỉ xem xét sắp xếp kiểu chọn cho danh sách liên tục. Giải thuật sau đây sử dụng hàm phụ trợ max_key của Sortable_list để tìm phần tử lớn nhất.
// Dành cho danh sách liên tục trong chương 4.
template <class Record>
void Sortable_list<Record>::selection_sort()
/*
post: Các phần tử trong danh sách đã được sắp xếp theo thứ tự không giảm.
uses: max_key, swap.
*/
{
for (int position = count - 1; position > 0; position--) {
int max = max_key(0, position);
swap(max, position);
}
}
Lưu ý rằng khi n-1 phần tử đã đứng vào vị trí đúng (n là số phần tử của danh
sách) thì phần tử còn lại đương nhiên có vị trí đúng. Do đó vòng lặp kết thúc tại
position==1.
template <class Record>
// Dành cho danh sách liên tục trong chương 4.
int Sortable_list<Record>::max_key(int low, int high)
/*
pre: low và high là hai vị trí hợp lệ trong danh sách và low <= high. post: trả về vị trí phần tử lớn nhất nằm trong khoảng chỉ số từ low đến high. uses: lớp Record.
*/
{
int largest, current;
largest = low;
for (current = low + 1; current <= high; current++)
if (entry[largest] < entry[current])
largest = current;
return largest;
}
template <class Record>
void Sortable_list<Record>::swap(int low, int high)
/*
pre: low và high là hai vị trí hợp lệ trong danh sách Sortable_list.
post: Phần tử tại low hoán đổi với phần tử tại high.
uses: Hiện thực danh sách liên tục trong chương 4.
*/
{
Record temp;
temp = entry[low]; entry[low] = entry[high]; entry[high] = temp;
}
Ưu điểm chính của sắp xếp kiểu chọn liên quan đến việc di chuyển dữ liệu.
Nếu một phần tử đã ở đúng vị trí của nó thì sẽ không bị di chuyển nữa. Khi hai
phần tử nào đó được đổi chỗ thì ít nhất một trong hai phần tử sẽ được đưa vào đúng vị trí cuối cùng của phần tử trong danh sách.
8.4. Shell_sort
Như chúng ta thấy, nguyên tắc hoạt động của sắp xếp kiểu chèn và sắp xếp kiểu chọn là ngược nhau. Sắp xếp kiểu chọn thực hiện việc di chuyển phần tử rất hiệu quả nhưng lại thực hiện nhiều phép so sánh thừa. Trong trường hợp tốt nhất có thể xảy ra, sắp xếp kiểu chèn thực hiện rất ít các phép so sánh nhưng lại thực hiện rất nhiều phép di chuyển dữ liệu thừa. Sau đây chúng ta xem xét một phương pháp trong đó nhược điểm của mỗi phương pháp trên sẽ được tránh càng nhiều càng tốt.
Lý do khiến giải thuật sắp xếp kiểu chèn chỉ di chuyển các phần tử mỗi lần được một vị trí là vì nó chỉ so sánh các phần tử gần nhau. Nếu chúng ta thay đổi giải thuật này sao cho nó so sánh các phần tử ở xa nhau trước thì khi có sự đổi chỗ, một phần tử sẽ di chuyển xa hơn. Dần dần, khoảng cách này được giảm dần đến 1 để đảm bảo rằng toàn bộ danh sách được sắp xếp. Đây cũng là tư tưởng của giải thuật Shell sort, được D.L. Shell đề xuất và hiện thực vào năm 1959. Phương pháp này đôi khi còn được gọi là phương pháp sắp xếp giảm độ tăng (diminishing-increment sort).
Ơ đây chúng ta xem một ví dụ khi sắp xếp các tên. Lúc đầu ta sắp xếp các tên ở cách nhau 5 vị trí, sau đó giảm xuống 3 và cuối cùng còn 1.
Mặc dù chúng ta phải duyệt danh sách nhiều lần, nhưng trong những lần duyệt trước các phần tử đã được di chuyển đến gần vị trí cuối cùng của chúng. Nhờ vậy những lần duyệt sau, các phần tử nhanh chóng được di chuyển về vị trí đúng sau cùng của chúng.
Các khoảng cách 5, 3, 1 được chọn ngẫu nhiên. Tuy nhiên, không nên chọn các bước di chuyển mà chúng lại là bội số của nhau. Vì khi đó thì các phần tử đã được so sánh với nhau ở bước trước sẽ được so sánh trở lại ở bước sau, mà như vậy vị trí của chúng sẽ không được cải thiện. Đã có một số nghiên cứu về Shell_sort, nhưng chưa ai có thể chỉ ra các khoảng cách di chuyển nào là tốt nhất. Tuy nhiên cũng có một số gợi ý về cách chọn các khoảng cách di chuyển. Nếu các khoảng di chuyển được chọn gần nhau thì sẽ phải duyệt danh sách nhiều lần hơn nhưng mỗi lần duyệt lại nhanh hơn. Ngược lại, nếu khoảng cách di chuyển giảm nhanh thì có ít lần duyệt hơn và mỗi lần duyệt sẽ tốn nhiều thời gian hơn. Điều quan trọng nhất là khoảng di chuyển cuối cùng phải là 1.
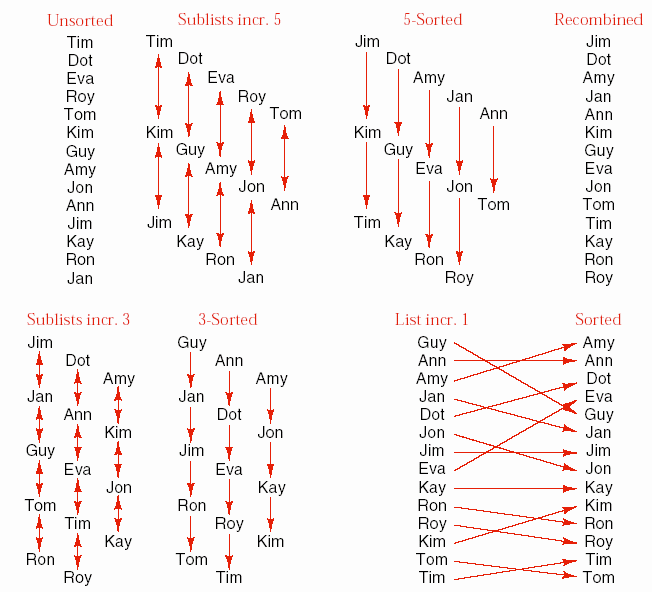
Hình 8.7 – Ví dụ về Shell_Sort.
template <class Record>
void Sortable_list<Record>::shell_sort()
/*
post: Các phần tử trong Sortable_list đã được sắp theo thứ tự khóa không giảm.
uses: Hàm sort_interval
*/
{
int increment = count; // Khoảng cách giữa các phần tử trong mỗi danh sách con.
int start;
do {
increment = increment / 3 + 1; // Giảm khoảng cách qua mỗi lần lặp.
for (start = 0; start < increment; start++)
sort_interval(start, increment);// Biến thể của giải thuật sắp xếp kiểu chèn.
} while (increment > 1);
}
Hàm sort_interval là một biến thể của giải thuật sắp xếp kiểu chèn, với
thông số increment là khoảng cách của hai phần tử kế nhau trong danh sách cần được sắp thứ tự. Tuy nhiên có một điều cần lưu ý là việc sắp xếp trong từng danh sách con không nhất thiết phải dùng phương pháp chen vào.
Tại bước cuối cùng, khoảng di chuyển là 1 nên Shell_sort về bản chất vẫn là sắp xếp kiểu chèn. Vì vậy tính đúng đắn của Shell_sort cũng tương tự như sắp xếp kiểu chèn. Về mặt hiệu quả, chúng ta hy vọng rằng các bước tiền xử lý sẽ giúp cho quá trình xử lý nhanh hơn.
Việc phân tích Shell_sort là đặc biệt khó. Cho đến nay, người ta chỉ mới có thể ước lượng được số lần so sánh và số phép gán cần thiết cho giải thuật trong những trường hợp đặc biệt.
8.5. Các phương pháp sắp xếp theo kiểu chia để trị
8.5.1. Ý tưởng cơ bản
Từ những giải thuật đã được trình bày và từ kinh nghiệm thực tế ta rút ra kết luận rằng sắp xếp danh sách dài thì khó hơn là sắp xếp danh sách ngắn. Nếu chiều dài danh sách tăng gấp đôi thì công việc sắp xếp thông thường tăng hơn gấp đôi (với sắp xếp kiểu chèn và sắp xếp kiểu chọn, khối lượng công việc tăng lên khoảng bốn lần). Do đó, nếu chúng ta có thể chia một danh sách ra thành hai phần có kích thước xấp xỉ nhau và thực hiện việc sắp xếp mỗi phần một cách riêng rẽ thì khối lượng công việc cần thiết cho việc sắp xếp sẽ giảm đi đáng kể. Ví dụ việc sắp xếp các phiếu trong thư viện sẽ nhanh hơn nếu các phiếu được chia thành từng nhóm có chung chữ cái đầu và từng nhóm được tiến hành sắp xếp riêng rẽ.
Ơ đây chúng ta vận dụng ý tưởng chia một bài toán thành nhiều bài toán tương tự như bài toán ban đầu nhưng nhỏ hơn và giải quyết các bài toán nhỏ này. Sau đó chúng ta tổng hợp lại để có lời giải cho toàn bộ bài toán ban đầu. Phương pháp này được gọi là “chia để trị” ( divide-and-conquer).
Để sắp xếp các danh sách con, chúng ta lại áp dụng chiến lược chia để trị để tiếp tục chia nhỏ từng danh sách con. Quá trình này dĩ nhiên không bị lặp vô tận. Khi ta có các danh sách con với kích thước là 1 phần tử thì quá trình dừng.
Chúng ta có thể thể hiện ý tưởng trên trong đoạn mã giả sau đây.
void Sortable_list::sort()
{
if (danh sách có nhiều hơn 1 phần tử)
{
Phân hoạch danh sách thành hai danh sách con lowlist, highlist;
lowlist.sort();
highlist.sort();
Kết nối hai danh sách con lowlist và highlist;
}
}
Vấn đề còn lại cần xem xét là cách phân hoạch (partition) danh sách ban đầu và cách kết nối (combine) hai danh sách đã có thứ tự cho thành một danh sách có thứ tự. Có hai phương pháp dưới đây, mỗi phương pháp sẽ làm việc tốt ứng với một số trường hợp riêng.
• Merge_sort: theo phương pháp này hai danh sách con chỉ cần có kích thước gần bằng nhau. Sau khi sắp xếp xong thì chúng được trộn lại sao cho danh sách cuối cùng có thứ tự.
• Quick_sort: theo phương pháp này, hai danh sách con được chia sao cho bước kết nối lại trở nên đơn giản. Phương pháp này được C. A. R. Hoare đưa ra. Để phân hoạch danh sách, chúng ta sẽ chọn một phần tử từ trong danh sách với hi vọng rằng có khoảng một nửa số phần tử đứng trước và khoảng một nửa số phần tử đứng sau phần tử được chọn trong danh sách có thứ tự sau cùng. Phần tử này được gọi là phần tử trụ (pivot). Sau đó chúng ta chia các phần tử theo qui tắc: các phần tử có khoá nhỏ hơn khoá của phần tử trụ được chia vào danh sách thứ nhất, các phần tử có khoá lớn hơn khoá của phần tử trụ được chia vào danh sách thứ hai. Khi hai danh sách này đã được sắp xếp thì chúng ta chỉ cần nối chúng lại với nhau.
8.5.2. Ví dụ
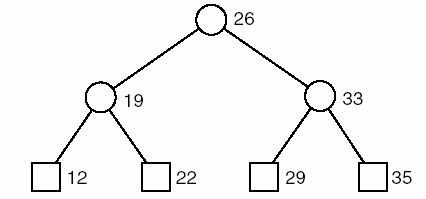
Trước khi xem xét chi tiết của các giải thuật, chúng ta sẽ thực hiện việc sắp xếp một danh sách cụ thể có 7 số như sau:
26 33 35 29 19 12 22
Hình 8.8- Cây đệ quy cho Merge_sort với 7 số.
8.5.2.1. Ví dụ cho Merge_sort
Bước đầu tiên là chia danh sách thành hai phần. Khi số phần tử của danh sách là lẻ thì chúng ta sẽ qui ước danh sách con bên trái sẽ dài hơn danh sách con bên phải một phần tử. Theo qui ước này, chúng ta có hai danh sách con
26 33 35 29 và 19 12 22
Ta xem xét danh sách con thứ nhất trước. Danh sách này cũng được chia thành hai phần
26 33 và 35 29
với mỗi nửa này, chúng ta lại áp dụng phương pháp trên để được các danh sách con có chiều dài là 1. Các danh sách con chiều dài 1 phần tử này không cần phải sắp xếp. Cuối cùng chúng ta cần phải trộn các danh sách con này để được một danh sách có thứ tự. 26 và 33 tạo thành danh sách 26 33; 35 và 29 được trộn thành 29 35. Kế tiếp, hai danh sách này này được trộn thành 26 29 33 35.
Tương tự như vậy, với nửa thứ hai của danh sách ban đầu ta được
Cuối cùng, trộn hai phần này ta được
12 19 22
12 19 22 26 29 33 35
8.5.2.2. Ví dụ cho Quick_sort
Chúng ta sử dụng ví dụ này cho Quick_sort.
Để sử dụng Quick_sort, trước tiên chúng ta phải xác định phần tử trụ. Phần tử này có thể là phần tử bất kỳ nào của danh sách, tuy nhiên, để cho thống nhất chúng ta sẽ chọn phần tử đầu tiên. Trong các ứng dụng thực tế thường người ta có những cách xác định phần tử trụ khác tốt hơn.
Theo ví dụ này, phần tử trụ đầu tiên là 26. Do đó hai danh sách con được tạo ra là:
19 12 22 và 33 35 29
Hai danh sách này lần lượt chứa các số nhỏ hơn và lớn hơn phần tử trụ. Ơ đây thứ tự của các phần tử trong hai danh sách con không đổi so với danh sách ban đầu nhưng đây không phải là điều bắt buộc.
Chúng ta tiếp tục sắp xếp các chuỗi con. Với chuỗi con thứ nhất, chúng ta chọn phần tử trụ là 19, do đó được hai danh sách con là 12 và 22. Hai danh sách này
chỉ có một phần tử nên đương nhiên có thứ tự. Cuối cùng, gom hai danh sách con và phần tử trụ lại ta có danh sách đã sắp xếp
12 19 22
Áp dụng phương pháp trên cho phần thứ hai của danh sách, ta được danh sách cuối cùng là
29 33 35
Gom hai danh sách con đã sắp xếp này và phần tử trụ đầu tiên ta được danh sách có thứ tự sau cùng:
12 19 22 26 29 33 35
Các bước của giải thuật được minh hoạ bởi hình sau.

Hình 8.9- Các bước thực thi của Quick_sort
Hình 8.10- Cây đệ quy cho Quick_sort với 7 phần tử.
8.6. Merge_sort cho danh sách liên kết
Sau đây là các hàm để thực hiện các phép sắp xếp nói trên. Với Merge_sort, chúng ta viết một phiên bản cho danh sách liên kết còn với Quick_sort thì chúng ta viết một phiên bản cho danh sách liên tục. Sinh viên có thể tự phân tích xem liệu cách làm ngược lại có khả thi và có hiệu quả hay không (Merge_sort cho danh sách liên tục và Quick_sort cho danh sách liên kết).
Merge_sort còn là một phương pháp rất tốt cho việc sắp xếp ngoại, tức là sắp xếp các dữ liệu nằm trên bộ nhớ ngoài có tốc độ truy xuất khá chậm và không có khả năng truy xuất ngẫu nhiên.
Sắp xếp danh sách liên kết có nghĩa là thay đổi các mối liên kết trong danh sách và tránh việc tạo mới hay xoá đi các phần tử. Cụ thể hơn, chương trình Merge_sort sẽ gọi một hàm đệ qui để xử lý từng tập con các phần tử của danh sách liên kết.
// Dành cho danh sách liên kết trong chương 4.
template <class Record>
void Sortable_list<Record>::merge_sort()
/*
post: Các phần tử trong danh sách đã được sắp theo thứ tự không giảm.
uses: recursive_merge_sort.
*/
{
recursive_merge_sort(head);
}
Sau đây là hàm recursive_merge_sort được viết dưới dạng đệ qui.
template <class Record>
void Sortable_list<Record>::recursive_merge_sort(Node<Record> *&sub_list)
/*
post: Các phần tử trong danh sách tham chiếu bởi sub_list đã được sắp theo thứ tự không
giảm. Tham biến con trỏ sub_list được cập nhật chứa địa chỉ phần tử đầu tiên và cũng là phần tử nhỏ nhất trong danh sách.
uses: Các hàm divide_from, merge, và recursive_merge_sort.
*/
{
if (sub_list != NULL && sub_list->next != NULL) { Node<Record> *second_half = divide_from(sub_list); recursive_merge_sort(sub_list); recursive_merge_sort(second_half);
sub_list = merge(sub_list, second_half);
}
}
Hàm đầu tiên mà hàm recursive_merge_sort sử dụng là divide_from.
Hàm này nhận vào danh sách được tham chiếu bởi sub_list và tách nó thành
hai nửa bằng cách thay liên kết ở giữa danh sách bằng NULL và trả về con trỏ đến phần tử đầu tiên của phần còn lại của danh sách ban đầu. Bằng cách cho con trỏ midpoint tiến một bước và con trỏ position tiến hai bước trong mỗi lần lặp, khi position đến cuối danh sách thì midpoint dừng ngay giữa danh sách.
// Dành cho danh sách liên kết trong chương 4.
template <class Record>
Node<Record> *Sortable_list<Record>::divide_from(Node<Record> *sub_list)
/*
post: Số phần tử trong danh sách trỏ bởi sub_list giảm một nửa. Địa chỉ phần tử đầu trong danh sách các phần tử còn lại được trả về. Nếu danh sách ban đầu có số phần tử lẻ thì danh sách thứ nhất nhiều hơn danh sách thứ hai 1 phần tử.
*/
{
Node<Record> *position,
*midpoint,
*second_half;
if ((midpoint = sub_list) == NULL) return NULL; // Danh sách ban đầu rỗng.
position = midpoint->next;
while (position != NULL) { // Tìm phần tử nằm giữa danh sách.
position = position->next;
if (position != NULL) { midpoint = midpoint->next; position = position->next;
}
}
second_half = midpoint->next;
midpoint->next = NULL;
return second_half;
}
Hàm thứ hai
Node<Record> *merge(Node<Record> *first, Node<Record> *second)
trộn hai danh sách có thứ tự không giảm trỏ bởi first và second thành một danh sách có thứ tự không giảm và trả về con trỏ đến phần tử có khoá nhỏ nhất (cũng là phần tử đầu tiên của danh sách kết quả). Hàm này duyệt đồng thời hai danh sách, so sánh một cặp khoá lấy từ hai phần tử, mỗi phần tử thuộc một trong hai danh sách nói trên, và đưa phần tử thích hợp (nhỏ hơn hoặc bằng) vào trong danh sách kết quả. Trường hợp đầu và cuối của danh sách cần phải được xử lý riêng biệt. Khi một trong hai danh sách hết trước, chúng ta chỉ cần nối phần còn lại của danh sách kia vào cuối danh sách kết quả. Cần nhắc lại rằng, đối với danh sách liên kết, cách xử lý cho phần tử đầu tiên không giống với cách xử lý cho các phần tử từ vị trí thứ hai trở đi, do có ảnh hưởng đến con trỏ đầu danh sách. Cách dễ dàng nhất là chúng ta tạo một nút tạm thời gọi là combined. Nút này được đặt ở đầu danh sách và không chứa dữ liệu thực. Với cấu trúc này, các phần tử có thể được đưa vào danh sách mà không cần phải phân biệt đâu là phần tử đầu tiên thực sự. Cuối cùng, giá trị trả về của hàm là con trỏ next của nút combined. Nút combined còn được gọi là nút giả vì nó không chứa dữ liệu thật sự mà chỉ được dùng để đơn giản hoá việc xử lý các con trỏ, nó sẽ không còn tồn tại khi hết phạm vi của phương thức merge.
Hình 8.11- Trôn hai danh sách đã có thứ tự.
// Dành cho danh sách liên kết trong chương 4.
template <class Record>
Node<Record> *Sortable_list<Record>::merge(Node<Record> *first,
Node<Record> *second)
/*
pre: first và second trỏ đến hai danh sách có thứ tự.
post: Phương thức trả về con trỏ trỏ đến danh sách các phần tử đã có thứ tự, đó là các phần tử của hai danh sách ban đầu được trộn lại. Hai danh sách ban đầu không còn phần tử.
uses: Các phương thức của lớp Records.
*/
{
Node<Record> *last_sorted;
Node<Record> combined; // Phần tử giả.
last_sorted = &combined; // Danh sách kết quả nhận dần các phần tử từ first và
// second, theo thứ tự từ phần tử nhỏ đến phần tử lớn.
while (first != NULL && second != NULL) {
if (first->entry <= second->entry) {
last_sorted->next = first;
last_sorted = first;
first = first->next;
}
else {
last_sorted->next = second;
last_sorted = second;
second = second->next;
}
}
// Nối phần còn lại của danh sách chưa hết.
if (first == NULL)
last_sorted->next = second;
else
last_sorted->next = first;
return combined.next;
}
8.7. Quick_sort cho danh sách liên tục
8.7.1. Các hàm
Giải thuật Quick_sort cho danh sách liên tục cần đến một giải thuật phân hoạch danh sách thông qua việc sử dụng phần tử trụ. Giải thuật này đổi chỗ các phần tử sao cho các phần tử có khoá nhỏ hơn khoá phần tử trụ sẽ được đứng trước, kế đến là các phần tử có khoá trùng với khoá của phần tử trụ, và cuối cùng là các phần tử có khoá lớn hơn khoá của phần tử trụ. Chúng ta dùng biến pivot_position để lưu lại vị trí của phần tử trụ trong danh sách đã được phân hoạch.
Do các danh sách con, kết quả của phép phân hoạch, được lưu trong cùng một danh sách và theo đúng vị trí tương đối giữa chúng, nên việc gom chúng lại thành một danh sách là hoàn toàn không cần thiết và chương trình không cần phải làm thêm bất cứ điều gì.
Để có thể gọi đệ qui hàm sắp xếp cho các danh sách con, các giới hạn trên và dưới của danh sách phải là các tham số cho hàm sắp xếp. Tuy nhiên, do qui ước của chúng ta là các phương thức sắp xếp không nhận tham số, chúng ta sẽ dùng một phương thức không có tham số để gọi hàm sắp xếp đệ qui có tham số.
// Dành cho danh sách liên tục trong chương 4.
template <class Record>
void Sortable_list<Record>::quick_sort()
/*
post: Các phần tử trong danh sách đã được sắp theo thứ tự không giảm.
uses: recursive_quick_sort.
*/
{
recursive_quick_sort(0, count - 1);
}
Hàm đệ qui thực hiện việc sắp xếp:
// Dành cho danh sách liên tục trong chương 4.
template <class Record>
void Sortable_list<Record>::recursive_quick_sort(int low, int high)
/*
pre: low và high là các vị trí hợp lệ trong Sortable_list.
post: Các phần tử trong danh sách từ chỉ số low đến chỉ số high đã được sắp theo thứ tự không giảm.
uses: recursive_quick_sort, partition.
*/
{
int pivot_position;
if (low < high) { // Danh sách có nhiều hơn một phần tử.
pivot_position = partition(low, high); recursive_quick_sort(low, pivot_position - 1); recursive_quick_sort(pivot_position + 1, high);
}
}
8.7.2. Phân hoạch danh sách
Có nhiều giải thuật để phân hoạch danh sách. Phương pháp chúng ta sử dụng ở đây rất đơn giản nhưng hiệu quả. Nó thực hiện số lần so sánh khoá nhỏ nhất có thể được.
8.7.2.1. Phát triển giải thuật
Cho giá trị của phần tử trụ, chúng ta phải bố trí lại các phần tử và tính chỉ số pivot_position sao cho phần tử trụ nằm tại pivot_position, các phần tử nhỏ hơn nằm phía bên trái và các phần tử lớn hơn nằm phía bên phải phần tử trụ. Để có thể xử lý trường hợp có nhiều hơn một phần tử có khoá đúng bằng khoá của phần tử trụ, chúng ta qui ước rằng các phần tử bên trái có khoá nhỏ hơn khoá của phần tử trụ một cách nghiêm ngặt trong khi các phần tử bên phải có khoá lớn hơn hoặc bằng khoá của phần tử trụ như trong sơ đồ sau đây.

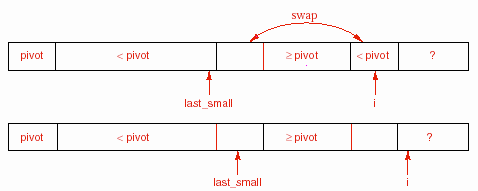
Để có được các phần tử như thế này, chúng ta phải so sánh từng phần tử với
phần tử trụ bằng cách sử dụng một vòng for với biến chỉ số là i. Ngoài ra, chúng ta còn sử dụng biến last_small sao cho các phần tử từ last_small trở về trước có khoá nhỏ hơn khoá của phần tử trụ. Giả sử ban đầu phần tử trụ nằm tại đầu

danh sách. Tạm thời chúng ta sẽ giữ nguyên vị trí của nó ở đó. Khi chương trình đang ở trong thân vòng lặp, danh sách và các biến có quan hệ với nhau như sau:
Khi chương trình kiểm tra phần tử tại vị trí i thì có hai trường hợp xảy ra. Nếu phần tử đó vẫn lớn hơn hay bằng phần tử trụ thì biến i sẽ tiếp tục tăng lên
và danh sách vẫn bảo toàn tính chất cần thiết. Ngược lại, chúng ta sẽ tăng
last_small và hoán đổi hai phần tử tại last_small (mới) và phần tử tại i. Khi đó, tính chất của danh sách vẫn được duy trì. Cuối cùng, khi i đã đi hết chiều dài của danh sách, chúng ta chỉ cần đổi chỗ phần tử trụ từ vị trí low sang vị trí last_small là sẽ có kết quả cần thiết.

8.7.2.2. Chọn phần tử trụ
Phần tử trụ không nhất thiết phải là phần tử đầu tiên của danh sách. Chúng ta có thể chọn bất cứ phần tử nào của danh sách để làm phần tử trụ. Thực tế thì phần tử đầu tiên thường không phải là phần tử trụ tốt. Vì nếu danh sách đã có thứ tự thì không có phần tử nào nhỏ hơn phần tử trụ, do đó một trong hai danh sách con sẽ rỗng và trong trường hợp này Quick_sort trở thành “Slow_sort”. Vì vậy, một lựa chọn tốt hơn cho phần tử trụ là phần tử gần giữa của danh sách với hi vọng rằng phần tử này sẽ chia hai danh sách có kích thước gần như nhau.
8.7.2.3. Viết chương trình
Với những lựa chọn này, chúng ta có được phương thức sau.
template <class Record>
int Sortable_list<Record>::partition(int low, int high)
/*
pre: low và high là các vị trí hợp lệ trong Sortable_list, low <= high.
post: Phần tử nằm giữa hai chỉ số low và high được chọn làm pivot. Các phần tử trong danh
sách từ chỉ số low đến chỉ số high đã được phân hoạch như sau: các phần tử nhỏ hơn pivot đứng trước pivot, các phần tử còn lại đứng saư pivot. Hàm trả về vị trí của pivot.
uses: các phương thức của lớp Record và hàm swap(int i, int j) hoán vị hai phần tử tại vị trí i và j trong danh sách.
*/
{
Record pivot;
int i, last_small;
swap(low, (low + high) / 2); pivot = entry[low]; last_small = low;
for (i = low + 1; i <= high; i++)
// Đầu mỗi lần lặp, chúng ta có các điều kiện sau:
// If low < j <= last_small then entry[j].key < pivot.
// If last_small < j < i then entry[j].key >= pivot.
if (entry[i] < pivot) { last_small = last_small + 1; swap(last_small, i);
}
swap(low, last_small);// Trả pivot về đúng vị trí thích hợp
return last_small;
}
8.8. Heap và Heap_sort
Quick_sort có một nhược điểm là độ phức tạp trong trường hợp xấu nhất rất lớn. Thông thường thì Quick_sort chạy rất nhanh nhưng cũng có những trường hợp dữ liệu vào khiến cho Quick_sort chạy rất chậm. Trong phần này chúng ta xem xét một phương pháp sắp xếp khác khắc phục được nhược điểm này. Giải thuật này có tên là Heap_sort. Heap_sort cần O(n log n) phép so sánh và di chuyển phần tử để sắp xếp một danh sách liên tục có n phần tử, ngay cả trong trường hợp xấu nhất. Như vậy trong trường hợp xấu nhất, Heap_sort có giới hạn
về thời gian chạy tốt hơn so với Quick_sort. Ngoài ra nó cũng tốt hơn
Merge_sort trên danh sách liên tục về mặt sử dụng không gian.
Giải thuật Heap_sort cũng như một số hiện thực của hàng ưu tiên trong chương 11 đều dựa trên cùng một khái niệm heap như nhau. Đó là một cấu trúc cây tương tự như cấu trúc cấp bậc trong một tổ chức. Chúng ta thường biểu diễn cấu trúc tổ chức của một công ty nào đó bằng một cấu trúc cây. Khi giám đốc công ty nghỉ việc thì một trong hai phó giám đốc (người tốt hơn, theo một số tiêu chí nào đó) sẽ được chọn để thế chỗ và như vậy tiếp tục trống một vị trí khác. Quá trình này được lặp lại từ chỗ cao nhất trong cấu trúc cho đến chỗ thấp nhất.
Chúng ta làm quen với định nghĩa heap nhị phân dưới đây.
8.8.1. Định nghĩa heap nhị phân
Định nghĩa: Một heap nhị phân là một cấu trúc cây nhị phân với hai tính chất sau:
1. Cây đầy đủ hoặc gần như đầy đủ.
2. Khóa tại mỗi nút đều nhỏ hơn hoặc bằng khóa của các nút trong hai cây con của nó.
Một cây nhị phân đầy đủ hoặc gần như đầy đủ chiều cao h sẽ có từ 2h-1 đến 2h-
1 nút. Do đó chiều cao của nó sẽ là O(logN).
Một điều quan trọng nhất ở đây là do tính chất cây đầy đủ hoặc gần như đầy đủ nên heap có thể được hiện thực bằng mảng liên tục các phần tử mà không cần
dùng đến con trỏ. Nếu phần tử đầu tiên của mảng có chỉ số là 0 thì, một phần tử tại vị trí i sẽ có con trái tại 2i+1 và con phải tại 2i+2, và cha của nó tại ⎣i-1/2⎦ .
13 13
(a) (b)
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
|
13
|
21
|
16
|
24
|
31
|
19
|
68
|
65
|
26
|
32
|
|
|
|
|
|
(c)
Hình 8.12 (a) Cây nhị phân gần như đầy đủ biểu diễn một heap.
(b) Không thỏa điều kiện của heap tại nét đứt rời.
(c) Hiện thực heap ở hình a trong một mảng liên tục.
Lưu ý rằng có khi chúng ta gọi heap được định nghĩa như trên là một min- heap, để phân biệt với trường hợp max-heap. Trong min-heap thì phần tử tại gốc là phần tử bé nhất. Max-heap sẽ sửa điều kiện thứ hai thành “Khóa tại mỗi nút đều lớn hơn hoặc bằng khóa của các nút trong hai cây con của nó”, do đó phần tử tại gốc sẽ là phần tử lớn nhất.
Max-heap được sử dụng trong giải thuật Heap_sort.
Khi đọc xong về hàng ưu tiên, sinh viên có thể thấy rằng có thể sử dụng ngay hàng ưu tiên (nếu đã có sẵn) để phục vụ cho việc sắp xếp theo đúng ý tưởng của Heap_sort. Tuy nhiên, nếu chỉ với mục đích hiện thực một giải thuật sắp thứ tự thật hiệu quả trên một danh sách sách liên tục, thì giải thuật sắp được trình bày dưới đây đơn giản và tiết kiệm không gian hơn rất nhiều, do nó đã cố gắng chỉ sửng dụng chính phần bộ nhớ chứa các phần tử cần sắp xếp, chứ không đòi hỏi thêm vùng nhớ nào đáng kể.
Hình 8.13- Max-heap biểu diễn dưới dạng cây và dưới dạng danh sách liên tục.
Lưu ý rằng heap không phải là một danh sách có thứ tự. Tuy phần tử đầu tiên
là phần tử lớn nhất của danh sách nhưng tại các vị trí k > 1 khác thì không có
một thứ tự bắt buộc giữa các phần tử k và k+1. Ngoài ra, từ heap ở đây không có liên hệ gì với từ heap dùng trong việc quản lý bộ nhớ động.
8.8.2. Phát triển giải thuật Heap_sort
8.8.2.1. Phương pháp
Giải thuật Heap_sort bao gồm hai giai đoạn. Đầu tiên, các phần tử trong danh sách được sắp xếp để thoả yêu cầu của một heap. Kế đến chúng ta lập lại nhiều lần việc lấy ra phần tử đầu tiên của heap và chọn một phần tử khác lên thay thế nó.
Trong giai đoạn thứ hai, chúng ta nhận thấy rằng gốc của cây (cũng là phần tử đầu tiên của danh sách hay là đỉnh của heap) là phần tử có khóa lớn nhất. Vị trí đúng cuối cùng của phần tử này là ở cuối danh sách. Như vậy chúng ta di chuyển phần tử này về cuối danh sách, phần tử tại vị trí cuối danh sách thì được chép vào phần tử tạm current để nhường chỗ. Kế đến chúng ta giảm biến last_unsorted là ranh giới giữa phần danh sách chưa được sắp xếp với các phần tử đã được đưa về vị trí đúng (Quá trình sắp xếp tiếp theo sẽ không quan tâm đến các phần tử nằm sau last_unsorted). Lúc này, vị trí đầu danh sách chưa sắp xếp được xem như trống, các phần tử còn lại trong danh sách đều đang thỏa điều kiện của heap. Việc cần làm chính là tìm chỗ thích hợp để đặt phần tử đang chứa tạm trong current vào danh sách này mà vẫn duy trì tính chất của heap, trước khi chọn ra phần tử lớn nhất kế tiếp. Hàm phụ trợ insert_heap sẽ làm điều này.
Như vậy, theo giải thuật này, Heap_sort cần truy xuất ngẫu nhiên đến các phần tử trong danh sách. Heap_sort chỉ thích hợp với danh sách liên tục.
8.8.2.2. Chương trình chính
Sau đây là hàm thực hiện giải thuật Heap_sort.
// Dành cho danh sách liên tục trong chương 4.
template <class Record>
void Sortable_list<Record>::heap_sort()
/*
post: Các phần tử trong danh sách đã được sắp xếp theo thứ tự không giảm.
uses: build_heap và insert_heap.
*/
{
Record current;
int last_unsorted; // Các phần tử nằm sau last_unsorted đã có thứ tự
build_heap(); // Giai đoạn 1: tạo heap từ danh sách các phần tử.
for (last_unsorted = count - 1; last_unsorted > 0; last_unsorted--)
{
current = entry[last_unsorted];
entry[last_unsorted] = entry[0];// Mỗi lần lặp chọn được một phần tử lớn nhất.
insert_heap(current, 0, last_unsorted - 1); // Khôi phục heap.
}
}
8.8.2.3. Ví dụ
Trước khi viết các hàm để tạo heap (build_heap) và đưa phần tử vào heap (insert_heap) chúng ta xem xét một số bước đầu tiên của quá trình sắp xếp heap trên hình.
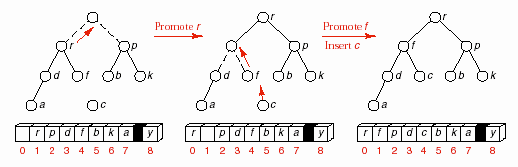
Hình 8.14 – Bước thứ nhất của Heapsort.
Trong bước đầu tiên, khoá lớn nhất, y, được di chuyển từ đầu đến cuối danh
sách. Hình vẽ đầu tiên cho thấy kết quả của việc di chuyển, trong đó y được tách ra khỏi cây và phần tử cuối cùng trước đây, c, được đưa vào phần tử tạm current.
Để tổ chức lại cây, chúng ta xem xét hai phần tử tại gốc của hai cây con. Mỗi phần tử này lớn hơn tất cả các phần tử khác trong cây con tương ứng. Do đó
chúng ta chọn phần tử lớn nhất trong ba phần tử, hai phần tử gốc của hai cây con và bản thân c, làm phần tử gốc mới của toàn bộ cây. Trong ví dụ này, chúng ta sẽ đưa phần tử r lên gốc và lặp lại quá trình cho hai cây con của r. Tới đây, chúng ta
sẽ dùng f để thế chỗ cho r. Tại f, vì f không có nút con cho nên c sẽ thế chỗ f và quá trình dừng.
Chúng ta thấy rằng điều kiện dừng khi tìm thấy chỗ trống thích hợp cho c thỏa tính chất của heap là: một chỗ trống mà không có nút con, hoặc một chỗ trống mà cả hai nút con đều <= c.
Tiếp theo, chúng ta lại có thể tách phần tử lớn nhất trong heap (phần tử đầu tiên) và lặp lại toàn bộ quá trình.
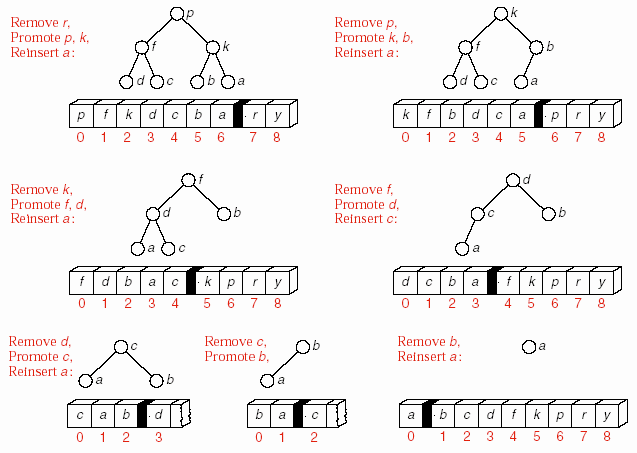
Hình 8. 15 – Theo vết của Heap_sort
8.8.2.4. Hàm insert_heap
Từ những điều trình bày ở trên ta có hàm insert_heap như sau.
// Dành cho danh sách liên tục trong chương 4.
template <class Record>
void Sortable_list<Record>::insert_heap(const Record ¤t, int low, int
high)
/*
pre: Các phần tử từ chỉ số low + 1 đến high thỏa điều kiện của heap. low xem như vị trí
còn trống (phần tử tại low sẽ bị bỏ đi).
post: Phần tử trong current thay thế cho phần tử tại low, và tất cả các phần tử từ low đến
high được tái sắp xếp để thỏa điều kiện của heap.
uses: Lớp Record
*/
{
int large;
large = 2 * low + 1; // large là vị trí con trái của low.
while (large <= high) {
if (large < high && entry[large] < entry[large + 1])
large++;//large là vị trí của con có khóa lớn nhất trong 2 con của phần tử tại low.
if (current >= entry[large])
break; // low chính là vị trí có thể đặt current vào.. else { // Dời phần tử con lên lấp chỗ trống.
entry[low] = entry[large];
low = large;
large = 2 * low + 1;
}
}
entry[low] = current;
}
8.8.2.5. Xây dựng heap ban đầu
Việc còn lại mà chúng ta phải làm là xây dựng heap ban đầu từ danh sách có thứ tự bất kỳ. Trước tiên, ta lưu ý rằng cây nhị phân có một số nút tự động thoả điều kiện của heap do chúng không có nút con. Đó chính là các nút lá trong cây. Do đó chúng ta không cần sắp xếp các nút lá của cây, tức là nửa sau của danh sách. Nếu chúng ta bắt đầu từ điểm giữa của danh sách và duyệt về phía đầu danh sách thì có thể sử dụng hàm insert_heap để đưa lần lượt từng phần tử vào trong heap, với lưu ý sử dụng các thông số low và high thích hợp.
// Dành cho danh sách liên tục trong chương 4.
template <class Record>
void Sortable_list<Record>::build_heap()
/*
post: Các phần tử trong danh sách được sắp xếp để thỏa điều kiện của heap.
uses: insert_heap.
*/
{
int low; // Các phần tử từ low+1 đến cuối danh sách thỏa điều kiện của heap.
for (low = count / 2 - 1; low >= 0; low--) {
Record current = entry[low];
insert_heap(current, low, count - 1);
}
}
8.9. Radix Sort
Cuối cùng chúng ta xem xét một giải thuật sắp thứ tự hơi đặc biệt một chút, đó là giải thuật thường được dùng cho các phần tử có khóa là các chuỗi ký tự. Giải thuật radix_sort vốn được đưa ra trong những ngày đầu của lịch sử máy tính để sử dụng cho các thẻ đục lỗ, nhưng đã được phát triển thành một phương pháp sắp thứ tự rất hiệu quả cho các cấu trúc dữ liệu có liên kết . Ý tưởng được trình bày dưới đây cũng được xem như một ứng dụng khá thú vị của hiện thực liên kết của CTDL hàng đợi.
8.9.1. Ý tưởng
Ý tưởng của giải thuật là xét từng ký tự một và chia danh sách thành nhiều danh sách con, số danh sách con phụ thuộc vào số ký tự khác nhau có trong khóa. Giả sử các khóa là các từ gồm các chữ cái, thì chúng ta chia danh sách cần sắp thứ tự ra 26 danh sách con tại mỗi bước và phân phối các phần tử vào các danh sách con này tương ứng với một trong các ký tự có trong khóa.
Để sắp thứ tự các từ, trước tiên người ta thường chia chúng thành 26 danh sách con theo ký tự đầu tiên, sau đó lại chia mỗi danh sách con thành 26 danh sách con theo ký tự thứ hai, và cứ thế tiếp tục. Như vậy số danh sách con sẽ trở nên quá lớn, chúng ta khó nắm giữ được. Ý tưởng dưới đây nhằm tránh số lượng danh sách con bùng nổ quá lớn. Thay vì lần lượt xét các ký tự từ trái qua phải, chúng ta sẽ xét theo thứ tự từ phải qua trái. Trước tiên nên chia các phần tử vào các danh sách con theo vị trí của ký tự cuối của từ dài nhất. Sau đó các danh sách con này lại được nối lại thành một danh sách, thứ tự các từ trong mỗi danh sách con giữ nguyên, thứ tự nối các danh sách con tuân theo thứ tự alphabet của các ký tự tại vị trí vừa xét. Danh sách này lại được chia theo vị trí kế trước vị trí vừa rồi, rồi lại được nối lại. Cứ thế tiếp tục cho đến khi danh sách được chia theo vị trí đầu tiên của các chuỗi ký tự và được nối lại, chúng ta sẽ có một danh sách các từ có thứ tự theo alphabet.
Quá trình này được minh họa qua việc sắp thứ tự 9 từ có chiều dài tối đa ba ký tự trong hình 8.16. Cột bên trái của hình vẽ là thứ tự ban đầu của các từ. Chúng được chia thành 3 danh sách tương ứng với 3 ký tự khác nhau ở vị trí cuối cùng, kết quả ở cột thứ hai của hình vẽ, mỗi hình khối biểu diễn một danh sách con. Thứ tự giữa các từ trong một danh sách con không thay đổi so với thứ tự giữa chúng trong danh sách lớn khi chưa được chia. Tiếp theo, các danh sách con được nối lại và được chia thành 2 danh sách con tương ứng 2 ký tự khác nhau ở vị trí kế cuối (vị trí thứ hai của từ) như cột thứ ba trong hình. Cuối cùng chúng được nối lại và chia thành 4 danh sách con tương ứng 4 ký tự khác nhau ở vị trí đầu của các từ. Khi các danh sách con được nối lại thì chúng ta có một danh sách đã có thứ tự.
8.9.2. Hiện thực
Chúng ta sẽ hiện thực phương pháp này trong C++ cho danh sách các mẫu tin có khóa là các chuỗi ký tự. Sau mỗi lần phân hoạch thành các danh sách con, chúng được nối lại thành một danh sách để sau đó lại được phân hoạch tiếp tương ứng với vị trí kế trước trong khóa. Chúng ta sử dụng các hàng đợi để chứa các danh sách con, do trong giải thuật, khi phân hoạch, các phần tử luôn được thêm vào cuối các danh sách con và khi nối lại thì các phần tử lại được lấy ra từ đầu các danh sách con (FIFO).
Nếu chúng ta dùng các CTDL hàng và danh sách tổng quát có sẵn để xử lý, sẽ có một số thao tác di chuyển các phần tử không cần thiết. Ngược lại, nếu sử dụng cấu trúc liên kết, có thể nối các hàng liên kết thành một danh sách kiên kết bằng cách nối rear của hàng này vào front của hàng kia, thì chương trình sẽ hiệu quả hơn rất nhiều. Quá trình này được minh họa trong hình 8.17. Chương trình radix_sort như vậy cần có thêm lớp dẫn xuất từ lớp Queue có bổ sung phương thức để nối các hàng lại với nhau, phần này có thể xem như bài tập. Phần minh họa tiếp theo chúng ta chỉ sử dụng lớp Queue đơn giản có sẵn.
Hình 8.16 – Tiến trình của radix_sort.
Chúng ta sẽ dùng một mảng có 28 hàng đợi để chứa 28 danh sách con. Vị trí 0
tương ứng ký tự trống (khoảng trắng không có ký tự), các vị trí từ 1 đến 26 tương ứng các ký tự chữ cái (không phân biệt chữ hoa chữ thường), còn vị trí 27 tương
ứng mọi ký tự còn lại (nếu có) xuất hiện trong khóa. Việc xử lý sẽ được lặp lại từ
ký tự cuối đến ký tự đầu trong khóa, mỗi lần lặp chúng ta sẽ duyệt qua danh sách liên kết để thêm từng phần tử vào cuối mỗi danh sách con tương ứng. Sau khi danh sách đã được phân hoạch, chúng ta nối các danh sách con lại thành một danh sách. Cuối vòng lặp danh sách đã có thứ tự.
Chúng ta sẽ hiện thực radix_sort như là một phương thức của
Sortable_list.
// Có thể sử dụng cho bất kỳ hiện thực nào của List.
template <class Record>
class Sortable_list: public List<Record> {
public: // Các phương thức sắp thứ tự.
void radix_sort();
private: // Các hàm phụ trợ.
void rethread(Queue queues[]);
};
Ở đây, lớp cơ sở List có thể là bất kỳ hiện thực nào của List trong chương 4.
Hàm phụ trợ rethread sẽ được sử dụng để nối các hàng đợi.
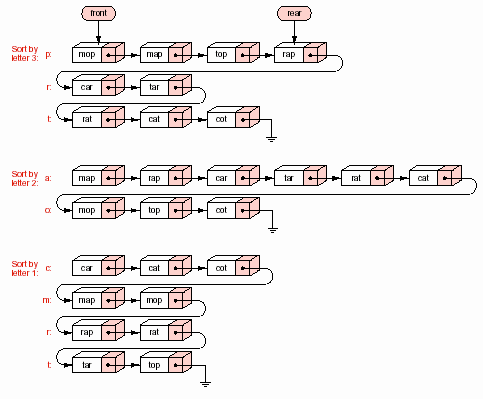
Hình 8.17 – Radix sort liên kết
Chúng ta sẽ sử dụng các phương thức của lớp Record, char key_letter(int
position) trả về ký tự tại position của khóa, hoặc trả về khoảng trắng nếu chiều dài của khóa nhỏ hơn position. Định nghĩa Record như sau:
class Record {
public:
char key_letter(int position) const;
Record(); // constructor mặc định.
operator Key() const; // trả về khóa của phần tử.
// Các phương thức và các thuộc tính khác của lớp.
};
8.9.2.1. Phương pháp sắp thứ tự radix_sort
const int max_chars = 28;
template <class Record>
void Sortable_list<Record>::radix_sort()
/*
post: Các phần tử của danh sách đã được sắp theo thứ tự alphabet.
uses: Các phương thức của các lớp List, Queue, và Record;
functions position and rethread.
*/
{
Record data;
Queue queues[max_chars];
for (int position = key_size - 1; position >= 0; position--) {
// Lặp từ vị trí cuối đến vị trí đầu các chuỗi ký tự.
while (remove(0, data) == success) {
int queue_number = alphabetic_order(data.key_letter(position));
queues[queue_number].append(data); // Đưa vào hàng thích hợp.
}
rethread(queues);// Nối các danh sách con trong các hàng thành danh sách.
}
}
Hàm này sử dụng hai hàm phụ trợ: alphabetic_order để xác định hàng đợi tương ứng với một ký tự cho trước, và Sortable_list::rethread() để nối các hàng. Chúng ta có thể dùng bất kỳ hiện thực nào của hàng tương thích với đặc tả Queue trừu tượng trong chương 3.
8.9.2.2. Chọn một queue
Hàm alphabetic_order lấy thứ tự của một ký tự cho trước trong bảng chữ cái, với quy ước rằng tất cả các ký tự không phải là ký tự chữ cái sẽ có cùng thứ tự là 27, khoảng trắng có thứ tự 0. Hàm không phân biệt chữ hoa và chữ thường.
int alphabetic_order(char c)
/*
post: Trả về thứ tự của ký tự trong c theo thứ tự alphabet, hoặc trả về 0 nếu c là khoảng trắng.
*/
{
if (c == ' ') return 0;
if ('a' <= c && c <= 'z') return c - 'a' + 1; if ('A' <= c && c <= 'Z') return c - 'A' + 1; return 27;
}
8.9.2.3. Nối các hàng
Hàm rethread nối 28 hàng lại thành một Sortable_list. Hàm cũng làm rỗng tất cả các hàng này để chúng có thể được sử dụng trong lần lặp sau của giải thuật. Hàm này có thể được viết lại theo cách phụ thuộc vào hiện thực của các hàng để giải thuật radix_sort có thể chạy nhanh hơn, chúng ta xem như bài tập.
template <class Record>
void Sortable_list<Record>::rethread(Queue queues[])
/*
post: Mọi hàng được nối lại thành một danh sách, các hàng trở thành rỗng.
uses: Các phương thức của các lớp List và Queue.
*/
{
Record data;
for (int i = 0; i < max_chars; i++)
while (!queues[i].empty()) { queues[i].retrieve(data); insert(size(), data); queues[i].serve();
}
}
8.9.3. Phân tích phương pháp radix_sort
Chú ý rằng thời gian để chạy radix_sort là (nk), n là số phần tử cần sắp thứ tự và k là số ký tự có trong khóa. Thời gian cần cho các phương pháp sắp thứ tự khác của chúng ta phụ thuộc vào n và không phụ thuộc trực tiếp vào chiều dài của khóa. Thời gian tốt nhất là đối với merge_sort: nlgn + O(n).
Hiệu quả tương đối của các phương pháp có liên quan đến kích thước nk và n lgn, có nghĩa là, k và lgn. Nếu các khóa có chiều dài lớn và số phần tử cần sắp thứ tự không lớn (k lớn và lg n tương đối nhỏ), thì các phương pháp khác, tựa như merge_sort, sẽ hiệu quả hơn radix_sort; ngược lại nếu k nhỏ (các khóa ngắn) và số phần tử cần sắp thứ tự nhiều, thì radix_sort sẽ nhanh hơn mọi phương pháp sắp thứ tự mà chúng ta đã biết.