 Chương 6 – ĐỆ QUY
Chương 6 – ĐỆ QUY
Chương này trình bày về đệ quy (recursion) – một phương pháp mà trong đó
để giải một bài toán, người ta giải các trường hợp nhỏ hơn của nó. Chúng ta cần tìm hiểu một vài ứng dụng và chương trình mẫu để thấy được một số trong rất nhiều dạng bài toán mà việc sử dụng đệ quy để giải rất có lợi. Một số ví dụ đơn giản, một số khác thực sự phức tạp. Chúng ta cũng sẽ phân tích xem đệ quy thường được hiện thực trong máy tính như thế nào, khi nào nên dùng đệ quy và khi nào nên tránh.
6.1. Giới thiệu về đệ quy
6.1.1. Cơ cấu ngăn xếp cho các lần gọi hàm
Khi một hàm gọi một hàm khác, thì tất cả các trạng thái mà hàm gọi đang có cần được khôi phục lại sau khi hàm được gọi kết thúc, để hàm này tiếp tục thực hiện công việc dở dang của mình. Trạng thái đó gồm có: điểm quay về (dòng lệnh kế sau lệnh gọi hàm); các trị trong các thanh ghi, vì các thanh ghi trong bộ xử lý sẽ được hàm được gọi sử dụng đến; các trị trong các biến cục bộ và các tham trị của nó. Như vậy mỗi hàm cần có một vùng nhớ dành riêng cho nó. Vùng nhớ này phải được tồn tại trong suốt thời gian kể từ khi hàm thực hiện cho đến khi nó kết thúc công việc.
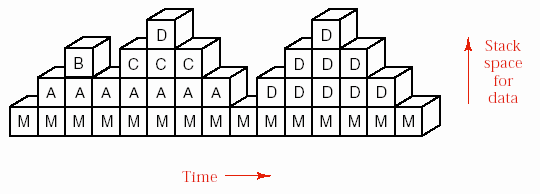
Hình 6.1- Cơ cấu ngăn xếp cho các lần gọi hàm
Giả sử chúng ta có ba hàm A, B, C, mà A gọi B, B gọi C. B sẽ không kết thúc trước khi C kết thúc. Tương tự, A khởi sự công việc đầu tiên nhưng lại kết thúc cuối cùng. Sự diễn tiến của các hoạt động của các hàm xảy ra theo tính chất vào sau ra trước (Last In First Out –LIFO). Nếu xét đến nhiệm vụ của máy tính trong việc tổ chức các vùng nhớ tạm dành cho các hàm này sử dụng, chúng ta thấy rằng các vùng nhớ này cũng phải nằm trong một danh sách có cùng tính chất trên, có nghĩa là ngăn xếp. Vì thế, ngăn xếp đóng một vai trò chủ chốt liên quan đến các hàm trong hệ thống máy tính. Trong hình 6.1, M biểu diễn chương trình chính, A, B, C là các hàm trên.
Hình 6.1 biểu diễn một dãy các vùng nhớ tạm cho các hàm, mỗi cột là hình ảnh của ngăn xếp tại một thời điểm, các thay đổi của ngăn xếp có thể được nhìn thấy bằng cách đọc từ trái sang phải. Hình ảnh này cũng cho chúng ta thấy rằng không có sự khác nhau trong cách đưa một vùng nhớ tạm vào ngăn xếp giữa hai trường hợp: một hàm gọi một hàm khác và một hàm gọi chính nó. Đệ quy là tên gọi trường hợp một hàm gọi chính nó, hay trường hợp các hàm lần lượt gọi nhau mà trong đó có một hàm gọi trở lại hàm đầu tiên. Theo cách nhìn của cơ cấu ngăn xếp, sự gọi hàm đệ quy không có gì khác với sự gọi hàm không đệ quy.
6.1.2. Cây biểu diễn các lần gọi hàm
Sơ đồ cây (tree diagram) có thể làm rõ hơn mối liên quan giữa ngăn xếp và việc gọi hàm. Sơ đồ cây hình 6.2 tương đương với cơ cấu ngăn xếp ở hình 6.1.
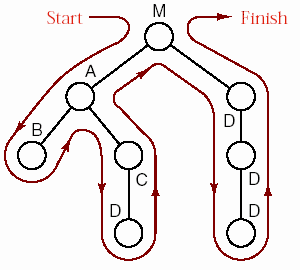
Hình 6.2- Cây biểu diễn các lần gọi hàm.
Chúng ta bắt đầu từ gốc của cây, tương ứng với chương trình chính. (Các thuật
ngữ dùng cho các thành phần của cây có thể tham khảo trong chương 9) Mỗi vòng tròn gọi là nút của cây, tương ứng với một lần gọi hàm. Các nút ngay dưới gốc cây biểu diễn các hàm được gọi trực tiếp từ chương trình chính. Mỗi hàm trong số trên có thể gọi hàm khác, các hàm này lại được biểu diễn bởi các nút ở sâu hơn. Bằng cách này cây sẽ lớn lên như hình 6.2 và chúng ta gọi cây này là cây biểu diễn các lần gọi hàm.
Để theo vết các lần gọi hàm, chúng ta bắt đầu từ gốc của cây và di chuyển qua hết cây theo mũi tên trong hình 6.2. Cách đi này được gọi là phép duyệt cây (traversal). Khi đi xuống và gặp một nút, đó là lúc gọi hàm. Sau khi duyệt qua hết phần cây bên dưới, chúng ta gặp trở lại nút này, đó là lúc kết thúc hàm được gọi. Các nút lá biểu diễn các hàm không gọi một hàm nào khác.
Chúng ta đặc biệt chú ý đến đệ quy, do đó thông thường chúng ta chỉ vẽ một phần của cây biểu diễn sự gọi đệ quy, và chúng ta gọi là cây đệ quy (recursion tree). Trong sơ đồ cây chúng ta cũng lưu ý một điều là không có sự khác nhau giữa cách gọi đệ quy với cách gọi hàm khác. Sự đệ quy đơn giản chỉ là sự xuất hiện của các nút khác nhau trong cây có quan hệ nút trước – nút sau với nhau mà có cùng tên. Điểm thứ hai cần lưu ý rằng, chính vì cây biểu diễn các lần gọi hàm, nên trong chương trình, nếu một lệnh gọi hàm chỉ xuất hiện một lần nhưng lại nằm trong vòng lặp, thì nút biểu diễn hàm sẽ xuất hiện nhiều lần trong cây, mỗi lần tương ứng một lần gọi hàm. Tương tự, nếu lệnh gọi hàm nằm trong phần rẽ nhánh của một điều kiện mà điều kiện này không xảy ra thì nút biểu diễn hàm sẽ không xuất hiện trong cây.
Cơ cấu ngăn xếp ở hình 6.1 cho thấy nhu cầu về vùng nhớ của đệ quy. Nếu một hàm gọi đệ quy chính nó vài lần thì bản sao của các biến khai báo trong hàm được tạo ra cho mỗi lần gọi đệ quy. Trong cách hiện thực thông thường của đệ quy, chúng được giữ trong ngăn xếp. Chú ý rằng tổng dung lượng vùng nhớ cần cho ngăn xếp này tỉ lệ với chiều cao của cây đệ quy chứ không phụ thuộc vào tổng số nút trong cây. Điều này có nghĩa rằng, tổng dung lượng vùng nhớ cần thiết để hiện thực một hàm đệ quy phụ thuộc vào độ sâu của đệ quy, không phụ thuộc vào số lần mà hàm được gọi.
Hai hình ảnh trên cho chúng ta thấy mối liên quan mật thiết giữa một biểu diễn cây và ngăn xếp:
Trong quá trình duyệt qua bất kỳ một cây nào, các nút được thêm vào hay lấy đi đúng theo kiểu của ngăn xếp. Trái lại, cho trước một ngăn xếp, có thể vẽ một cây để mô tả quá trình thay đổi của ngăn xếp.
Chúng ta hãy tìm hiểu một vài ví dụ đơn giản về đệ quy. Sau đó chúng ta sẽ xem xét đệ quy thường được hiện thực trong máy tính như thế nào.
6.1.3. Giai thừa: Một định nghĩa đệ quy
Trong toán học. giai thừa của một số nguyên thường được định nghĩa bởi công thức:
Hoặc định nghĩa sau:
n! = n x (n-1) x ... x 1.
1 nếu n=0
 n! =
n! =
n x (n-1)! nếu n>0.
Giả sử chúng ta cần tính 4!. Theo định nghĩa chúng ta có:
4! = 4 x 3!
= 4 x (3 x 2!)
= 4 x (3 x (2 x 1!))
= 4 x (3 x (2 x (1 x 0!)))
= 4 x (3 x (2 x (1 x 1)))
= 4 x (3 x (2 x 1))
= 4 x (3 x 2)
= 4 x 6
= 24
Việc tính toán trên minh họa bản chất của cách mà đệ quy thực hiện. Để có được câu trả lời cho một bài toán lớn, phương pháp chung là giảm bài toán lớn thành một hoặc nhiều bài toán con có bản chất tương tự mà kích thước nhỏ hơn. Sau đó cũng chính phương pháp chung này lại được sử dụng cho những bài toán con, cứ như thế đệ quy sẽ tiếp tục cho đến khi kích thước của bài toán con đã giảm đến một kích thước nhỏ nhất nào đó của một vài trường hợp cơ bản, mà lời giải của chúng có thể có được một cách trực tiếp không cần đến đệ quy nữa. Nói cách khác:
Mọi quá trình đệ quy gồm có hai phần:
• Một vài trường hợp cơ bản nhỏ nhất có thể được giải quyết mà không cần đệ quy.
• Một phương pháp chung có thể giảm một trường hợp thành một hoặc nhiều trường hợp nhỏ hơn, và nhờ đó việc giảm nhỏ vấn đề có thể tiến triển cho đến kết quả cuối cùng là các trường hợp cơ bản.
C++, cũng như các ngôn ngữ máy tính hiện đại khác, cho phép đệ quy dễ dàng. Việc tính giai thừa trong C++ trở thành một hàm sau đây.
int factorial(int n)
/*
pre: n là một số không âm.
post: trả về trị của n giai thừa.
*/
{
if (n == 0)
return 1;
else
return n * factorial(n - 1);
}
Như chúng ta thấy, định nghĩa đệ quy và lời giải đệ quy của một bài toán đều có thể rất ngắn gọn và đẹp đẽ. Tuy nhiên việc tính toán chi tiết có thể đòi hỏi phải giữ lại rất nhiều phép tính từng phần trước khi có được kết quả đầy đủ.
Máy tính có thể dễ dàng nhớ các tính toán từng phần bằng một ngăn xếp. Con người thì khó làm được như vậy, con người khó có thể nhớ một dãy dài các kết quả tính toán từng phần để rồi sau đó quay lại hoàn tất chúng. Do đó, khi sử dụng đệ quy, cách chúng ta suy nghĩ có khác với các cách lập trình khác. Chúng ta phải xem xét vấn đề bằng một cách nhìn tổng thể và dành những việc tính toán chi tiết lại cho máy tính.
Chúng ta phải đặc tả trong giải thuật của chúng ta một cách chính xác các bước tổng quát của việc giảm một bài toán lớn thành nhiều trường hợp nhỏ hơn; chúng ta phải xác định điều kiện dừng (các trường hợp nhỏ nhất) và cách giải của chúng. Ngoại trừ một số ít ví dụ nhỏ và đơn giản, chúng ta không nên cố gắng hiểu giải thuật đệ quy bằng cách biến đổi từ bài toán ban đầu cho đến tận bước kết thúc, hoặc lần theo vết của các công việc mà máy tính sẽ làm. Làm như thế, chúng ta sẽ nhanh chóng lẫn lộn bởi các công việc bị trì hoãn lại và chúng ta sẽ bị mất phương hướng.
6.1.4. Chia để trị: Bài toán Tháp Hà Nội
6.1.4.1. Bài toán
Vào thế kỷ thứ 19 ở châu Âu xuất hiện một trò chơi được gọi là Tháp Hà Nội. Người ta kể rằng trò chơi này biểu diễn một nhiệm vụ ở một ngôi đền của Ấn Độ giáo. Vào cái ngày mà thế giới mới được tạo nên, các vị linh mục được giao cho 3 cái tháp bằng kim cương, tại tháp thứ nhất có để 64 cái đĩa bằng vàng. Các linh mục này phải di chuyển các đĩa từ tháp thứ nhất sang tháp thứ ba sao cho mỗi lần chỉ di chuyển 1 đĩa và không có đĩa lớn nằm trên đĩa nhỏ. Người ta bảo rằng khi công việc hoàn tất thì đến ngày tận thế.
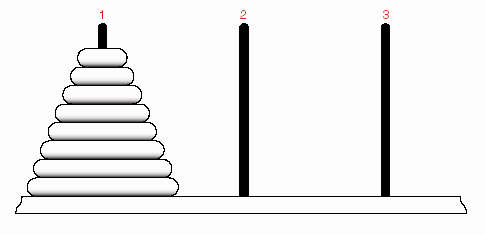
Hình 6.3- Bài toán tháp Hà nội
Nhiệm vụ của chúng ta là viết một chương trình in ra các bước di chuyển các đĩa giúp cho các nhà linh mục, chúng ta gọi dòng lệnh sau
move(64, 1, 3, 2)
có nghĩa là: chuyển 64 đĩa từ tháp thứ nhất sang tháp thứ ba, sử dụng tháp thứ hai làm nơi để tạm.
6.1.4.2. Lời giải
Ý tưởng để đến với lời giải ở đây là, sự tập trung chú ý của chúng ta không phải là vào bước đầu tiên di chuyển cái đĩa trên cùng, mà là vào bước khó nhất: di chuyển cái đĩa dưới cùng. Đĩa lớn nhất dưới cùng này sẽ phải có vị trí ở dưới cùng tại tháp thứ ba theo yêu cầu bài toán. Không có cách nào khác để chạm được đến đĩa cuối cùng trước khi 63 đĩa nằm trên đã được chuyển đi. Đồng thời 63 đĩa này phải được đặt tại tháp thứ hai để tháp thứ ba trống.
Chúng ta đã có được một bước nhỏ để tiến đến lời giải, đây là một bước rất nhỏ vì chúng ta còn phải tìm cách di chuyển 63 đĩa. Tuy nhiên đây lại là một bước rất quan trọng, vì việc di chuyển 63 đĩa đã có cùng bản chất với bài toán ban đầu, vì không có lý do gì ngăn cản việc chúng ta di chuyển 63 đĩa này theo cùng một cách tương tự.
move(63,1,2,3);// Chuyển 63 đĩa từ tháp 1 sang tháp 2 (tháp 3 dùng làm nơi để tạm). cout << "Chuyển đĩa thứ 64 từ tháp 1 sang tháp 3." << endl; move(63,2,3,1);// Chuyển 63 đĩa từ tháp 2 sang tháp 3 (tháp 1 dùng làm nơi để tạm).
Cách suy nghĩ như trên chính là ý tưởng của đệ quy. Chúng ta đã mô tả các bước chủ chốt được thực hiện như thế nào, và các công việc còn lại của bài toán cũng sẽ được thực hiện một cách tương tự. Đây cũng là ý tưởng của việc chia để trị: để giải quyết một bài toán, chúng ta chia công việc ra thành nhiều phần nhỏ hơn, mỗi phần lại được chia nhỏ hơn nữa, cho đến khi việc giải chúng trở nên dễ dàng hơn bài toán ban đầu rất nhiều.
6.1.4.3. Tinh chế
Để viết được giải thuật, chúng ta cần biết tại mỗi bước, tháp nào được dùng để chứa tạm các đĩa. Chúng ta có đặc tả sau đây cho hàm:
void move(int count, int start, int finish, int temp);
pre: Có ít nhất là count đĩa tại tháp start. Đĩa trên cùng của tháp temp và tháp finish lớn
hơn bất kỳ đĩa nào trong count đĩa trên cùng tại tháp start.
post: count đĩa trên cùng tại tháp start đã được chuyển sang tháp finish; tháp temp được
dùng làm nơi để tạm sẽ trở lại trạng thái ban đầu.
Giả sử rằng bài toán của chúng ta sẽ dừng sau một số bước hữu hạn (mặc dầu đó có thể là ngày tận thế!), và như vậy phải có cách nào đó để việc đệ quy dừng lại. Một điều kiện dừng hiển nhiên là khi không còn đĩa cần di chuyển nữa. Chúng ta có thể viết chương trình sau:
const int disks = 64; // Cần sửa hằng số này thật nhỏ để chạy thử chương trình.
void move(int count, int start, int finish, int temp);
/*
pre: Không có.
post: Chương trình mô phỏng bài toán Tháp Hà Nội kết thúc.
*/
main()
{
move(disks, 1, 3, 2);
}
Hàm đệ quy như sau:
void move(int count, int start, int finish, int temp)
{
if (count > 0) {
move(count - 1, start, temp, finish);
cout << "Move disk " << count << " from " << start
<< " to " << finish << "." << endl;
move(count - 1, temp, finish, start);
}
}
6.1.4.4. Theo vết của chương trình
Công cụ hữu ích của chúng ta trong việc tìm hiểu một hàm đệ quy là hình ảnh thể hiện các bước thực hiện của nó trên một ví dụ thật nhỏ. Các lần gọi hàm trong hình 6.4 là cho trường hợp số đĩa bằng 2. Mỗi khối trong sơ đồ biểu diễn những gì diễn ra trong một lần gọi hàm. Lần gọi ngoài cùng move(2,1,3,2) (do chương trình chính gọi) có ba dòng lệnh sau:
move(1,1,2,3);// Chuyển 1 đĩa từ tháp 1 sang tháp 2 (tháp 3 dùng làm nơi để tạm). cout << " Chuyển đĩa thứ 2 từ tháp 1 sang tháp 3." << endl; move(1,2,3,1);// Chuyển 1 đĩa từ tháp 2 sang tháp 3 (tháp 1 dùng làm nơi để tạm).
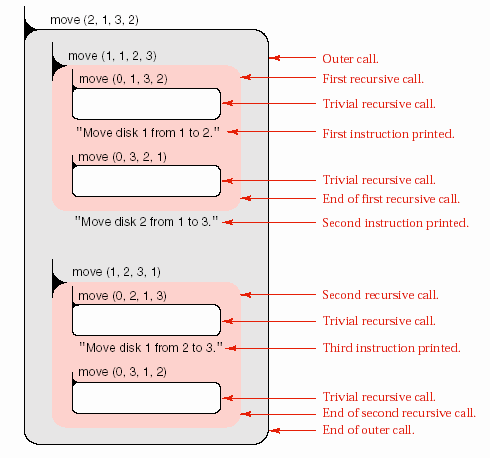
Hình 6.4- Theo vết của chương trình Tháp Hà Nội với số đĩa là 2.
Dòng lệnh thứ nhất và dòng lệnh thứ ba gọi đệ quy. Dòng lệnh move(1,1,2,3)
bắt đầu gọi hàm move thực hiện trở lại dòng lệnh đầu tiên, nhưng với các thông số mới. Dòng lệnh này sẽ thực hiện đúng ba lệnh sau:
move(0,1,3,2);// Chuyển 0 đĩa (gọi đệ quy lần nữa, biểu diễn bởi khối nhỏ bên
/ / trong).
cout << "Chuyển đĩa 1 từ tháp 1 sang tháp 2" << endl;
move(0,3,2,1);// Chuyển 0 đĩa (gọi đệ quy lần nữa, biểu diễn bởi khối nhỏ bên
/ / trong).
Sau khi khối biểu diễn lần gọi đệ quy này kết thúc, dòng lệnh hiển thị "Chuyển đĩa thứ 2 từ tháp 1 sang tháp 3" thực hiện. Sau đó là khối biểu diễn lần gọi đệ quy move(1,2,3,1).
Chúng ta thấy rằng hai lần gọi đệ quy bên trong khối move(1,1,2,3) có số đĩa là 0 nên không phải thực hiện điều gì, hình biễu diễn là một khối rỗng. Giữa hai lần này là hiểu thị "Chuyển đĩa 1 từ tháp 1 sang tháp 2." Tương tự cho các dòng lệnh bên trong move(1,2,3,1), chúng ta hiểu được cách mà đệ quy hiện thực.
Chúng ta sẽ xem xét thêm một công cụ khác có tính hiển thị cao hơn trong việc biểu diễn sự đệ quy bằng cách lần theo vết của chương trình vừa rồi.
6.1.4.5. Phân tích
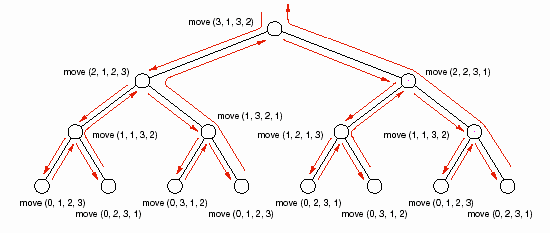
Hình 6.5- Cây đệ quy cho trường hợp 3 đĩa
Hình 6.5 là cây đệ quy cho bài toán Tháp Hà Nội với 3 đĩa.
Lưu ý rằng chương trình của chúng ta cho bài toán Tháp Hà Nội không chỉ sinh ra một lời giải đầy đủ cho bài toán mà còn sinh ra một lời giải tốt nhất có thể có, và đây cũng là lời giải duy nhất được tìm thấy trừ khi chúng ta chấp nhận lời giải với một dãy dài lê thê các bước dư thừa và bất lợi như sau:
Chuyển đĩa 1 từ tháp 1 sang tháp 2. Chuyển đĩa 1 từ tháp 2 sang tháp 3. Chuyển đĩa 1 từ tháp 3 sang tháp 1. . . .
Để chứng minh tính duy nhất của một lời giải không thể giản lược hơn được nữa, chúng ta chú ý rằng, tại mỗi bước, nhiệm vụ cần làm được tổng kết lại là cần di chuyển một số đĩa nhất định nào đó từ một tháp này sang một tháp khác. Không có cách nào khác ngoài cách là trước hết phải di chuyển toàn bộ số đĩa bên trên, trừ đĩa cuối cùng nằm dưới, sau đó có thể thực hiện một số bước dư thừa nào đó, tiếp theo là di chuyển chính đĩa cuối cùng, rồi lại có thể thực hiện một số bước dư thừa nào đó, để cuối cùng là di chuyển toàn bộ số đĩa cũ về lại trên đĩa dưới cùng này. Như vậy, nếu loại đi tất cả các việc làm dư thừa thì những việc còn lại chính là cốt lõi của giải thuật đệ quy của chúng ta.
Tiếp theo, chúng ta sẽ tính xem đệ quy được gọi liên tiếp bao nhiêu lần trước khi có sự quay về. Lần đầu đệ quy có count=64, mỗi lần đệ quy count được giảm đi 1. Vậy nếu chúng ta gọi đệ quy với count = 0, lần đệ quy này không thực hiện gì, chúng ta có tổng độ sâu của đệ quy là 64. Điều này có nghĩa rằng, nếu chúng ta vẽ cây đệ quy cho chương trình, thì cây sẽ có 64 mức không kể mức của
các mức lá. Ngoại trừ các nút lá, các nút khác đều gọi đệ quy hai lần trong mỗi nút, như vậy tổng số nút tại mỗi mức chính xác bằng hai lần tổng số nút ở mức cao hơn.
Từ cách suy nghĩ trên về cây đệ quy (ngay cả khi cây quá lớn không thể vẽ được), chúng ta có thể dễ dàng tính ra số lần di chuyển cần làm (mỗi lần di chuyển một đĩa) để di chuyển hết 64 đĩa theo yêu cầu bài toán. Mỗi nút trong cây sẽ in một lời hướng dẫn tương ứng một lần chuyển một đĩa, trừ các nút lá. Tổng số nút gốc và nút trung gian là:
1 +2 +4 +... +263 = 20 +21 +22 +... +263 = 264 -1.
nên số lần di chuyển đĩa cần thực hiện tất cả là 264 –1. Chúng ta có thể ước chừng con số này lớn như thế nào bằng cách so sánh với
103 = 1000 ≈ 1024 = 210,
ta có tổng số lần di chuyển đĩa bằng 264 =24 x 260 ≈24 x 1018 =1.6 x1019
Mỗi năm có khoảng 3.2 x 107 giây. Giả sử mỗi lần di chuyển một đĩa được thực hiện mất 1 giây, thì toàn bộ công việc của các linh mục sẽ phải thực hiện mất 5 x 1011 năm. Các nhà thiên văn học ước đoán tuổi thọ của vũ trụ sẽ nhỏ hơn 20 tỉ năm, như vậy, theo truyền thuyết của bài toán này thì thế giới còn kéo dài hơn cả việc tính toán đó đến 25 lần!
Không có một máy tính nào có thể chạy được chương trình Tháp Hà Nội, do không đủ thời gian, nhưng rõ ràng không phải là do vấn đề không gian. Không gian ở đây chỉ đòi hỏi 64 lần gọi đệ quy.
6.2. Các nguyên tắc của đệ quy
6.2.1. Thiết kế giải thuật đệ quy
Đệ quy là một công cụ cho phép người lập trình tập trung vào bước chính yếu của giải thuật mà không phải lo lắng tại thời điểm khởi đầu về cách kết nối bước chính yếu này với các bước khác. Khi cần giải quyết một vấn đề, bước tiếp cận đầu tiên nên làm thường là xem xét một vài ví dụ đơn giản, và chỉ sau khi đã hiểu được chúng một cách kỹ lưỡng, chúng ta mới thử cố gắng xây dựng một phương pháp tổng quát hơn. Một vài điểm quan trọng trong việc thiết kế một giải thuật đệ quy được liệt kê sau đây:
Tìm bước chính yếu. Hãy bắt đầu bằng câu hỏi “Bài toán này có thể được chia nhỏ như thế nào?” hoặc “Bước chính yếu trong giai đoạn giữa sẽ được thực hiện
như thế nào?”. Nên đảm bảo rằng câu trả lời của bạn đơn giản nhưng có tính tổng quát. Không nên đi từ điểm khởi đầu hay điểm kết thúc của bài toán lớn, hoặc sa vào quá nhiều trường hợp đặc biệt (do chúng chỉ phù hợp với các bài toán nhỏ). Khi đã có được một bước nhỏ và đơn giản để hướng tới lời giải, hãy tự hỏi rằng những khúc mắc còn lại của bài toán có thể được giải quyết bằng cách tương tự hay không, để sửa lại phương pháp của bạn cho tổng quát hơn, nếu cần thiết. Ngoại trừ những định nghĩa toán học thể hiện sự đệ quy quá rõ ràng, một điều thú vị mà chúng ta sẽ lần lượt gặp trong những chương sau là, khi những bài toán cần được giải quyết trên những cấu trúc dữ liệu mà định nghĩa mang tính chất đệ quy như danh sách, chuỗi ký tự biểu diễu biểu thức số học, cây, hay đồ thị,… thì giải pháp hướng tới một giải thuật đệ quy là rất dễ nhìn thấy.
Tìm điều kiện dừng. Điều kiện dừng chỉ ra rằng bài toán hoặc một phần nào đó của bài toán đã được giải quyết. Điều kiện dừng thường là trường hợp nhỏ, đặc biệt, có thể được giải quyết một cách dễ dàng không cần đệ quy.
Phác thảo giải thuật. Kết hợp điều kiện dừng với bước chính yếu của bài toán, sử dụng lệnh if để chọn lựa giữa chúng. Đến đây thì chúng ta có thể viết hàm đệ quy, trong đó mô tả cách mà bước chính yếu được tiến hành cho đến khi gặp được điều kiện dừng. Mỗi lần gọi đệ quy hoặc là phải giải quyết một phần của bài toán khi gặp một trong các điều kiện dừng, hoặc là phải giảm kích thước bài toán hướng dần đến điều kiện dừng.
Kiểm tra sự kết thúc. Kế tiếp, và cũng là điều tối quan trọng, là phải chắc chắn việc gọi dệ quy sẽ không bị lặp vô tận. Bắt đầu từ một trường hợp chung, qua một số bước hữu hạn, chúng ta cần kiểm tra liệu điều kiện dừng có khả năng xảy ra để quá trình đệ quy kết thúc hay không. Trong bất kỳ một giải thuật nào, khi một lần gọi hàm không phải làm gì, nó thường quay về một cách êm thấm. Đối với giải thuật đệ quy, điều này rất thường xảy ra, do việc gọi hàm mà không phải làm gì thường là một điều kiện dừng. Do đó, cần lưu ý rằng việc gọi hàm mà không làm gì thường không phải là một lỗi trong trường hợp của hàm đệ quy.
Kiểm tra lại mọi trường hợp đặc biệt
Cuối cùng chúng ta cũng cần bảo đảm rằng giải thuật của chúng ta luôn đáp ứng mọi trường hợp đặc biệt.
Vẽ cây đệ quy. Công cụ chính để phân tích các giải thuật đệ quy là cây đệ quy. Như chúng ta đã thấy trong bài toán Tháp Hà Nội, chiều cao của cây đệ quy liên quan mật thiết đến tổng dung lượng bộ nhớ mà chương trình cần đến, và kích thước tổng cộng của cây phản ánh số lần thực hiện bước chính yếu và cũng là tổng thời gian chạy chương trình. Thông thường chúng ta nên vẽ cây đệ quy cho
một hoặc hai trường hợp đơn giản của bài toán của chúng ta vì nó sẽ chỉ dẫn cho chúng ta nhiều điều.
6.2.2. Cách thực hiện của đệ quy
Câu hỏi về cách hiện thực của một chương trình đệ quy trong máy tính cần được tách rời khỏi câu hỏi về sử dụng đệ quy để thiết kế giải thuật.
Trong giai đoạn thiết kế, chúng ta nên sử dụng mọi phương pháp giải quyết vấn đề mà chúng tỏ ra thích hợp với bài toán, đệ quy là một trong các công cụ hiệu quả và linh hoạt này.
Trong giai đoạn hiện thực, chúng ta cần tìm xem phương pháp nào trong số các phương pháp sẽ là tốt nhất so với từng tình huống.
Có ít nhất hai cách để hiện thực đệ quy trong hệ thống máy tính. Quan điểm chính của chúng ta khi xem xét hai cách hiện thực khác nhau dưới đây là, cho dù có sự hạn chế về không gian và thời gian, chúng cũng nên được tách riêng ra khỏi quá trình thiết kế giải thuật. Các loại thiết bị tính toán khác nhau trong tương lai có thể dẫn đến những khả năng và những hạn chế khác nhau. Chúng ta sẽ tìm hiểu hai cách hiện thực đa xử lý và đơn xử lý của đệ quy dưới đây.
6.2.2.1. Hiện thực đa xử lý: sự đồng thời
Có lẽ rằng cách suy nghĩ tự nhiên về quá trình hiện thực của đệ quy là các hàm không chiếm những phần riêng trong cùng một máy tính, mà chúng sẽ được thực hiện trên những máy khác nhau. Bằng cách này, khi một hàm cần gọi một hàm khác, nó khởi động chiếc máy tương ứng, và khi máy này kết thúc công việc, nó sẽ trả về chiếc máy ban đầu kết quả tính được để chiếc máy ban đầu có thể tiếp tục công việc. Nếu một hàm gọi đệ quy chính nó hai lần, đơn giản nó chỉ cần khởi động hai chiếc máy khác để thực hiện cũng những dòng lệnh y như những dòng lệnh mà nó đang thực hiện. Khi hai máy này hoàn tất công việc chúng trả kết quả về cho máy gọi chúng. Nếu chúng cần gọi đệ quy, dĩ nhiên chúng cũng khởi động những chiếc máy khác nữa.
Thông thường bộ xử lý trung ương là thành phần đắt nhất trong hệ thống máy tính, nên bất kỳ một ý nghĩ nào về một hệ thống có nhiều hơn một bộ xử lý cũng cần phải xem xét đến sự lãng phí. Nhưng rất có thể trong tương lai chúng ta sẽ thấy những hệ thống máy tính lớn chứa hàng trăm, nếu không là hàng ngàn, các bộ vi xử lý tương tự trong các thành phần của nó. Khi đó thì việc thực hiện đệ quy bằng nhiều bộ xử lý song song sẽ trở nên bình thường.
Với đa xử lý, những người lập trình sẽ không còn xem xét các giải thuật chỉ như một chuỗi tuyến tính các hành động, thay vào đó, cần phải nhận ra một số phần của giải thuật có thể thực hiện song song. Cách xử lý này còn được gọi là xử
lý đồng thời (concurrent). Việc nghiên cứu về xử lý đồng thời và các phương pháp kết nối giữa chúng hiện tại là một đề tài nghiên cứu trong khoa học máy tính, một điều chắc chắn là nó sẽ cải tiến cách mà các giải thuật sẽ được mô tả và hiện thực trong nhiều năm tới.
6.2.2.2. Hiện thực đơn xử lý: vấn đề vùng nhớ
Để xem xét làm cách nào mà đệ quy có thể được thực hiện trong một hệ thống chỉ có một bộ xử lý, chúng ta nhớ lại cơ cấu ngăn xếp của các lần gọi hàm đã được giới thiệu ở đầu chương này. Một hàm khi được gọi cần phải có một vùng nhớ riêng để chứa các biến cục bộ và các tham trị của nó, kể cả các trị trong các thanh ghi và địa chỉ quay về khi nó chuẩn bị gọi một hàm khác. Sau khi hàm kết thúc, nó sẽ không còn cần đến bất cứ thứ gì trong vùng nhớ dành riêng cho nó nữa. Thực sự là không có sự khác nhau giữa việc gọi một hàm đệ quy và việc gọi một hàm không đệ quy. Khi một hàm chưa kết thúc, vùng nhớ của nó là bất khả xâm phạm. Một lần gọi hàm đệ quy cũng là một lần gọi hàm riêng biệt. Chúng ta cần chú ý rằng hai lần gọi đệ quy là hoàn toàn khác nhau, để chúng ta không trộn lẫn vùng nhớ của chúng khi chúng chưa kết thúc. Đối với những hàm đệ quy, những thông tin lưu trữ dành cho lần gọi ngoài cần được giữ cho đến khi nó kết thúc, như vậy một lần gọi bên trong phải sử dụng một vùng khác làm vùng nhớ của riêng nó.
Đối với một hàm không đệ quy, vùng nhớ có thể là một vùng cố định và được dành cho lâu dài, do chúng ta biết rằng một lần gọi hàm sẽ được trả về trước khi hàm có thể lại được gọi lần nữa, và sau khi lần gọi trước được trả về, các thông tin trong vùng nhớ của nó không còn cần thiết nữa. Vùng nhớ lâu dài được dành sẵn cho các hàm không đệ quy có thể gây lãng phí rất lớn, do những khi hàm không được yêu cầu thực hiện, vùng nhớ đó không thể được sử dụng vào mục đích khác. Đó cũng là cách quản lý vùng nhớ dành cho các hàm của các phiên bản cũ của các ngôn ngữ như FORTRAN và COBOL, và chính điều này cũng là lý do mà các ngôn ngữ này không cho phép đệ quy.
6.2.2.3. Nhu cầu về thời gian và không gian của một quá trình đệ quy
Chúng ta hãy xem lại cây biểu diễn các lần gọi hàm: trong quá trình duyệt cây, các nút được thêm vào hay lấy đi đúng theo kiểu của ngăn xếp. Quá trình này được minh họa trong hình 6.1.
Từ hình này, chúng ta có thể kết luận ngay rằng tổng dung lượng vùng nhớ cần để hiện thực đệ quy tỉ lệ thuận với chiều cao của cây đệ quy. Những người lập
trình không tìm hiểu kỹ về đệ quy thỉnh thoảng vẫn nhầm lẫn rằng không gian cần phải có liên quan đến tổng số nút trong cây. Thời gian chạy chương trình liên quan đến số lần gọi hàm, đó là tổng số nút trong cây; nhưng dung lượng vùng nhớ
tại một thời điểm chỉ là tổng các vùng nhớ dành cho các nút nằm trên đường đi từ nút tương ứng với hàm đang thực thi ngược về gốc của cây. Không gian cần
thiết được phản ánh bởi chiều cao của cây. Một cây đệ quy có nhiều nút nhưng không cao thể hiện một quá trình đệ quy mà nó thực hiện được rất nhiều công việc trên một vùng nhớ không lớn.
6.2.3. Đệ quy đuôi
Chúng ta hãy xét đến trường hợp hành động cuối cùng trong một hàm là việc gọi đệ quy chính nó. Hãy xem xét ngăn xếp dành cho quá trình đệ quy, như chúng ta thấy, các thông tin cần để khôi phục lại trạng thái cho lần đệ quy ngoài sẽ được lưu lại ngay trước khi lần đệ quy trong được gọi. Tuy nhiên khi lần đệ quy trong thực hiện xong thì lần đệ quy ngoài cũng không còn việc gì phải làm nữa, do việc gọi đệ quy là hành động cuối cùng của hàm nên đây cũng là lúc mà hàm đệ quy ngoài kết thúc. Và như vậy việc lưu lại những thông tin dùng để khôi phục trạng thái cũ của lần đệ quy ngoài trở nên hoàn toàn vô ích. Mọi việc cần làm ở đây chỉ là gán các trị cần thiết cho các biến và quay ngay trở về đầu hàm, các biến được gán trị y như là chính hàm đệ quy bên trong nhận được qua danh sách thông số vậy. Chúng ta tổng kết nguyên tắc này như sau:
Nếu dòng lệnh sẽ được chạy cuối cùng trong một hàm là gọi đệ quy chính nó, thì việc gọi đệ quy này có thể được loại bỏ bằng cách gán lại các thông số gọi theo các giá trị như là đệ quy vẫn được gọi, và sau đó lập lại toàn bộ hàm.
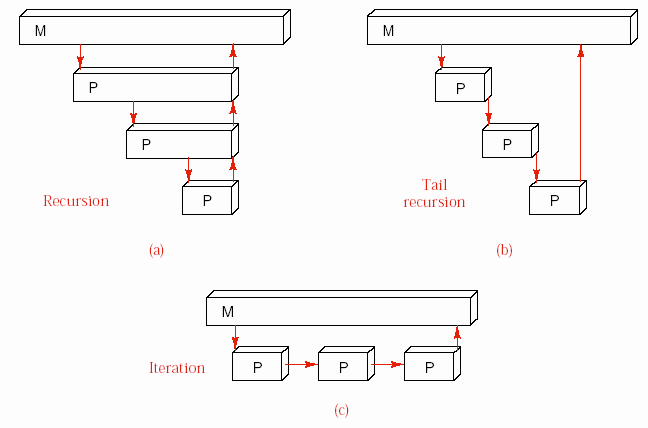
Hình 6.6 – Đệ quy đuôi
Quá trình thay đổi này được minh họa trong hình 6.6. Hình 6.6a thể hiện vùng nhớ được sử dụng bởi chương trình gọi M và một số bản sao của hàm đệ quy P, mỗi hàm một vùng nhớ riêng. Các mũi tên xuống thể hiện sự gọi hàm. Mỗi sự gọi từ P đến chính nó cũng là hành động cuối trong hàm, việc duy trì vùng nhớ cho hàm trong khi chờ đợi sự trả về từ hàm được gọi là không cần thiết. Cách biến đổi như trên sẽ giảm kích thước vùng nhớ đáng kể (hình 6.6b). Cuối cùng, hình 6.6c biểu diễn các lần gọi hàm P như một dạng lặp lại trong cùng một mức của sơ đồ.
Trường hợp đặc biệt chúng ta vừa nêu trên là vô cùng quan trọng vì nó cũng thường xuyên xảy ra. Chúng ta gọi đó là trường hợp đệ quy đuôi (tail recursion). Chúng ta nên cẩn thận rằng trong đệ quy đuôi, việc gọi đệ quy là hành động cuối trong hàm, chứ không phải là dòng lệnh cuối được viết trong hàm. Trong chương trình có khi chúng ta thấy đệ quy đuôi xuất hiện trong lệnh switch hoặc lệnh if trong hàm mà sau đó còn có thể có nhiều dòng lệnh khác nữa.
Đối với phần lớn các trình biên dịch, chỉ có một sự khác nhau nhỏ giữa thời gian chạy trong hai trường hợp: trường hợp đệ quy đuôi và trường hợp nó đã được thay thế bằng vòng lệnh lặp. Tuy nhiên, nếu không gian được xem là quan trọng, thì việc loại đệ quy đuôi là rất cần thiết. Đệ quy đuôi thường được thay bởi vòng lặp while hoặc do while.
Trong giải thuật chia để trị của bài toán Tháp Hà Nội, lần gọi đệ quy trên không phải là đệ quy đuôi, lần gọi sau đó mới là đệ quy đuôi. Hàm sau đây đã được loại đệ quy đuôi:
void move(int count, int start, int finish, int temp)
/* move: phiên bản lặp.
pre: count là số đĩa cần di chuyển.
post: count đĩa đã được chuyển từ start sang finish dùng temp làm nơi chứa tạm.
*/
{
int swap;
while (count > 0) { // Thay lệnh if trong đệ quy bằng vòng lặp.
move(count - 1, start, temp, finish);// lần gọi đệ quy đầu không phải
// đệ quy đuôi.
cout << "Move disk " << count << " from " << start
<< " to " << finish << "." << endl;
count--; // Thay đổi các thông số cho tương đương với việc gọi đệ quy đuôi.
swap = start; start = temp; temp = swap;
}
}
Thật ra chúng ta có thể nghĩ ngay đến phương án này khi mới bắt đầu giải bài toán. Nhưng chúng ta đã xem xét nó từ một cách nhìn khác, bây giờ chúng ta sẽ lý giải lại các dòng lệnh trên một cách tự nhiên hơn. Chúng ta sẽ thấy rằng hai tháp start và temp không có gì khác nhau, do chúng cùng được sử dụng để làm nơi chứa tạm trong khi chúng ta chuyển dần các đĩa về tháp finish.
Để chuyển một số đĩa từ start về finish, chúng ta chuyển tất cả đĩa trong số
đó, trừ cái cuối cùng, sang tháp còn lại là temp. Sau đó chuyển đĩa cuối sang
finish.
Tiếp tục lặp lại việc vừa rồi, chúng ta lại cần chuyển tất cả các đĩa từ temp, trừ cái cuối cùng, sang tháp còn lại là start, để có thể chuyển đĩa cuối cùng sang finish. Lần thực hiện thứ hai này sử dụng lại các dòng lệnh trong chương trình bằng cách hoán đổi start với temp. Cứ như thế, sau mỗi lần hoán đổi start với temp, công việc được lặp lại y như nhau, kết quả của mỗi lần lặp là chúng ta có được thêm một đĩa mới trên finish.
6.2.4. Phân tích một số trường hợp nên và không nên dùng đệ quy
6.2.4.1. Giai thừa
Chúng ta hãy xem xét hai hàm tính giai thừa sau đây. Đây là hàm đệ quy:
int factorial(int n)
/* factorial: phiên bản đệ quy.
pre: n là một số không âm.
post: trả về trị của n giai thừa.
*/
{
if (n == 0) return 1;
else return n * factorial(n - 1);
}
Và đây là hàm không đệ quy:
int factorial(int n)
/* factorial: phiên bản không đệ quy.
pre: n là một số không âm.
post: trả về trị của n giai thừa.
*/
{
int count, product = 1;
for (count = 1; count <= n; count++)
product *= count;
return product;
}
Chương trình nào trên đây sử dụng ít vùng nhớ hơn? Với cái nhìn đầu tiên,
dường như chương trình đệ quy chiếm ít vùng nhớ hơn, do nó không có biến cục bộ, còn chương trình không đệ quy có đến hai biến cục bộ. Tuy nhiên, chương
trình đệ quy cần một ngăn xếp để chứa n con số
n, n-1, n-2, ..., 2, 1
là những thông số để gọi đệ quy (hình 6.7), và theo cách đệ quy của mình, nó cũng phải nhân các số lại với nhau theo một thứ tự không khác gì so với chương trình không đệ quy. Tiến trình thực hiện của chương trình đệ quy cho n = 5 như sau:
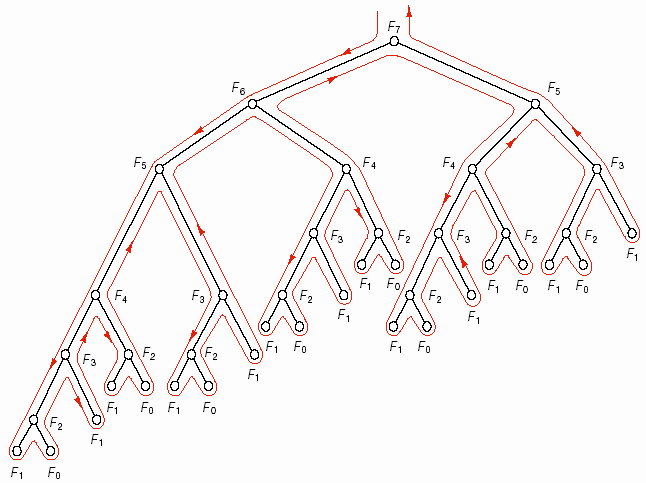
Hình 6.7 –
Cây đệ quy tính giai thừa
factorial(5) =5*factorial(4)
=5*(4*factorial(3))
=5*(4*(3*factorial(2)))
=5*(4*(3*(2*factorial(1))))
=5*(4*(3*(2*(1*factorial(0)))))
=5*(4*(3*(2*(1*1))))
=5*(4*(3*(2*1)))
=5*(4*(3*2))
=5*(4*6)
=5*24
=120
Như vậy chương trình đệ quy chiếm nhiều vùng nhớ hơn chương trình không đệ
quy, đồng thời nó cũng chiếm nhiều thời gian hơn do chúng vừa phải cất và lấy các trị từ ngăn xếp vừa phải thực hiện việc tính toán.
6.2.4.2. Các số Fibonacci
Một ví dụ còn lãng phí hơn chương trình tính giai thừa là việc tính các số
Fibonacci. Các số này được định nghĩa như sau:
F0 = 0, F1 = 1, Fn = Fn-1 + Fn-2 nếu n ≥2. Chương trình đệ quy tính các số Fibonacci rất giống với định nghĩa:
int fibonacci(int n)
/* fibonacci: phiên bản đệ quy.
pre: n là một số không âm.
post: trả về số Fibonacci thứ n.
*/
{
if (n <= 0) return 0;
else if (n == 1) return 1;
else return fibonacci(n - 1) + fibonacci(n - 2);
}
Thực tế, chương trình này trông rất đẹp mắt, do nó có dạng chia để trị: kết quả có được bằng cách tính toán hai trường hợp nhỏ hơn. Tuy nhiên, chúng ta sẽ thấy rằng đây hoàn toàn không phải là trường hợp “chia để trị”, mà là “chia làm cho phức tạp thêm”.
ình 6.8- Cây đệ quy tính F7.
Để xem xét giải thuật này, chúng ta thử tính F7, minh họa trong hình 6.8.
Trước hết hàm cần tính F6 và F5. Để có F6, phải có F5 và F4, và cứ như thế tiếp
tục. Nhưng sau khi F5 được tính để có được F6, thì F5 sẽ không được giữ lại. Như
vậy để tính F7 sau đó, F5 lại phải được tính lại. Cây đệ quy đã cho chúng ta thấy
rất rõ rằng chương trình đệ quy phải lập đi lập lại nhiều phép tính một cách
không cần thiết.Tổng thời gian để hàm đệ quy tính được Fn là một hàm mũ của n.
Cũng giống như việc tính giai thừa, chúng ta có thể có được một chương trình đơn giản bằng cách giữ lại ba biến, đó là trị của số Fibonacci mới nhất và hai số Fibonacci kế trước:
int fibonacci(int n)
/* fibonacci: phiên bản không đệ quy.
pre: n là một số không âm.
post: trả về số Fibonacci thứ n.
*/
{
|
int
|
current;
|
//
|
số Fibonacci hiện tại Fi
|
|
int
|
last_value;
|
//
|
Fi-1
|
|
int
|
last_but_one;
|
//
|
Fi-2
|
if (n <= 0) return 0;
else if (n == 1) return 1;
else {
last_but_one = 0;
last_value = 1;
for (int i = 2; i <= n; i++) {
current = last_but_one + last_value;
last_but_one = last_value;
last_value = current;
}
return current;
}
}
Chương trình không đệ quy này có thời gian chạy tỉ lệ với n.
6.2.4.3. So sánh giữa đệ quy và không đệ quy
Đâu là điều khác nhau cơ bản giữa chương trình vừa rồi với chương trình đệ quy? Để trả lời câu hỏi này, chúng ta hãy xem xét lại cây đệ quy. Việc phân tích cây đệ quy sẽ đem lại nhiều thông tin hữu ích giúp chúng ta biết được khi nào thì nên sử dụng đệ quy và khi nào thì không.
Nếu một hàm gọi đệ quy chính nó chỉ có một lần thì cây đệ quy sẽ có dạng rất đơn giản: đó là một chuỗi các mắc xích, có nghĩa là, mỗi nút chỉ có duy nhất một con. Nút con này tương ứng với một lần gọi đệ quy. Đối với hàm giai thừa, đó chỉ đơn giản là một danh sách các yêu cầu việc tính toàn các số giai thừa từ (n-1)! cho đến 1!. Bằng cách đọc cây đệ quy từ dưới lên trên thay vì từ trên xuống dưới, chúng ta có ngay chương trình không đệ quy từ một chương trình đệ quy. Khi một cây suy giảm thành một danh sách, việc chuyển từ chương trình đệ quy thành chương trình không đệ quy thường dễ dàng, và kết quả có được thường tiết kiệm cả không gian lẫn thời gian.
Lưu ý rằng một hàm gọi đệ quy chính bản thân nó có thể có nhiều dạng khác nhau. Dòng gọi đệ quy hoặc là chỉ xuất hiện một lần trong một vòng lặp nhưng thực sự lại được gọi nhiều lần, hoặc là xuất hiện hai lần trong lệnh rẽ nhánh if, else nhưng thực sự chỉ được thực hiện có một lần.
Cây đệ quy tính các số Fibonacci không phải là một chuỗi các mắc xích. Nó chứa một số rất lớn các nút biểu diễn những công việc được lặp lại. Khi chương trình đệ quy chạy, nó tạo một ngăn xếp để sử dụng trong khi duyệt qua cây. Tuy nhiên, các kết quả lưu vào ngăn xếp khi lấy ra chỉ được sử dụng có một lần và sẽ bị mất đi mà không thể sử dụng lại (vì đỉnh ngăn xếp sau khi được truy xuất cần được loại bỏ mới có thể truy xuất tiếp những phần tử khác trong ngăn xếp), và như vậy một công việc nào đó có thể phải được thực hiện nhiều lần.
Trong những trường hợp như vậy, tốt hơn hết là thay ngăn xếp bằng một cấu trúc dữ liệu khác, một cấu trúc dữ liệu mà cho phép truy nhập vào nhiều vị trí khác nhau thay vì chỉ ở đỉnh như ngăn xếp. Trong ví dụ đơn giản về các số Fibonacci, chúng ta chỉ cần thêm hai biến tạm để chứa hai trị cần cho việc tính số mới.
Cuối cùng, khác với việc một chương trình đệ quy tự tạo cho mình một ngăn xếp riêng, bằng cách tạo một ngăn xếp tường minh, chúng ta luôn có thể chuyển mọi chương trình đệ quy thành chương trình không đệ quy. Chương trình không đệ quy thường phức tạp và khó hiểu hơn. Nếu một chương trình đệ quy có thể chạy được với một không gian và thời gian cho phép, thì chúng ta không nên khử đệ quy trừ trường hợp ngôn ngữ lập trình mà chúng ta sử dụng không có khả năng đệ quy.
6.2.4.4. So sánh giữa Fibonacci và Tháp Hà Nội: kích thước của lời giải
Hàm đệ quy tính các số Fibonacci và hàm đệ quy giải bài toán Tháp Hà Nội đều có dạng chia để trị rất giống nhau. Mỗi hàm đều gọi đệ quy chính nó hai lần cho các trường hợp nhỏ hơn. Tuy nhiên, vì sao chương trình Tháp Hà Nội lại vô cùng hiệu quả trong khi chương trình tính các số Fibonacci lại hoàn toàn ngược lại? Câu trả lời liên quan đến kích thước của lời giải. Để tính một số Fibonacci, rõ ràng kết quả mà chúng ta cần chỉ có mỗi một số, và chúng ta mong muốn việc tính toán sẽ hoàn tất qua một số ít các bước, như là các dòng lệnh trong chương trình không đệ quy. Trong khi đó, chương trình đệ quy Fibonacci lại thực hiện quá nhiều bước. Trong chương trình Tháp Hà Nội, ngược lại, kích thước của lời giải là số các lời chỉ dẫn cần in ra cho các linh mục và là một hàm mũ của tổng số đĩa.
6.2.5. Các nhận xét
Để đi đến kết luận về giải pháp lựa chọn cho một chương trình đệ quy hay không đệ quy, điểm bắt đầu tốt nhất cũng là xem xét cây đệ quy. Nếu cây đệ quy có dạng đơn giản, chương trình không đệ quy sẽ tốt hơn. Nếu cây chứa nhiều công việc được lặp lại mà các cấu trúc dữ liệu khác thích hợp hơn là ngăn xếp, thì đệ quy cũng không còn cần thiết nữa. Nếu cây đệ quy thực sự “rậm rạp”, mà trong đó số công việc lặp lại không đáng kể, thì chương trình đệ quy là giải pháp tốt nhất.
Ngăn xếp được sử dụng khi đệ quy (do chương trình đệ quy tự tạo lấy) được xem như một danh sách chứa các công việc cần trì hoãn của chương trình. Nếu danh sách này có thể được tạo trước, thì chúng ta nên viết chương trình không đệ quy, ngược lại, chúng ta sẽ viết chương trình đệ quy. Đệ quy như một cách tiếp cận từ trên xuống khi cần giải quyết vấn đề, nó chia bài toán thành những bài toán nhỏ hơn, hoặc chọn ra bước chủ yếu và trì hoãn các bước còn lại. Chương trình không đệ quy gần với cách tiếp cận từ dưới lên, nó bắt đầu từ những cái đã biết và từng bước xây dựng nên lời giải.
Một chương trình đệ quy luôn có thể được thay thế bởi một chương trình không đệ quy có sử dụng ngăn xếp. Điều ngược lại cũng luôn đúng: một chương trình không đệ quy có sử dụng ngăn xếp có thể được thay bởi chương trình đệ quy không có ngăn xếp. Do đó, không những người lập trình thường phải tự hỏi có nên khử đệ quy hay không, mà đôi khi chính họ lại cần đặt câu hỏi ngược lại, có nên chuyển thành đệ quy một chương trình không đệ quy có sử dụng ngăn xếp hay không. Điều thứ hai này có thể dẫn đến một chương trình gần với bản chất tự nhiên của bài toán hơn và do đó dễ hiểu hơn. Đó cũng là một cách để cải tiến cách tiếp cận bài toán cũng như các kết quả đạt được.
Có một số lời khuyên trong việc sử dụng đệ quy, đó là chúng ta không nên dùng đệ quy khi câu trả lời cho bất kỳ câu hỏi nào dưới đây đều là không:
• Bản thân giải thuật hoặc cấu trúc dữ liệu có tính chất đệ quy một cách tự nhiên?
• Lời giải đệ quy ngắn gọn và dễ hiểu hơn?
• Lời giải đệ quy đòi hỏi một không gian và thời gian chấp nhận được?
Các bước gợi ý trong việc khử đệ quy đuôi
1. Sử dụng một biến để thay thế cho việc gọi đệ quy trở lại.
2. Sử dụng một vòng lặp với điều kiện kết thúc giống như điều kiện dừng của
đệ quy.
3. Đặt tất cả các lệnh vốn cần thực hiện trong lần gọi đệ quy đuôi vào trong vòng lặp.
4. Thay lệnh gọi đệ quy bằng một phép gán.
5. Dùng các lệnh gán để gán các trị như là các thông số mà hàm đệ quy lẽ ra
nhận được.
6. Trả về trị cho biến đã định nghĩa ở bước 1.
Các bước gợi ý trong việc khử đệ quy một cách tổng quát
Chúng ta có thể tạo một ngăn xếp để chứa các bản ghi. Lệnh goi đệ quy và lệnh trả về từ hàm đệ quy có thể dược thay thế như sau. Mỗi lệnh gọi đệ quy có thể được thay bởi:
1. Đưa vào ngăn xếp một bản ghi chứa các biến cục bộ, các thông số và vị trí dòng lệnh ngay sau lệnh gọi đệ quy.
2. Gán mọi thông số về các trị mới thích hợp.
3. Trở về thực hiện dòng lệnh đầu tiên trong giải thuật đệ quy.
4. Mỗi lệnh trả về của hàm đệ quy được thay bởi:
5. Lấy từ ngăn xếp để khôi phục mọi biến cục bộ và thông số.
6. Bắt đầu thực hiện dòng lệnh tại vị trí mà trước đó đã được cất trong ngăn
xếp.
6.3. Phương pháp quay lui (backtracking)
Như một ứng dụng khá phức tạp về đệ quy, chúng ta hãy xem xét một câu đố rất phổ biến về việc làm cách nào để đặt tám con hậu trên một bàn cờ có tám hàng và tám cột sao cho chúng không thể nhìn thấy nhau. Theo luật của bàn cờ thì một con hậu có thể nhìn thấy những con cờ khác nằm trên hàng, hoặc cột, hoặc hai đường chéo có chứa nó.
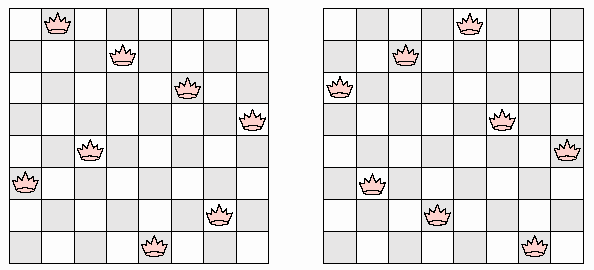
Hình 6.9- Hai cấu hình thỏa điều kiện của bài toán tám con hậu.
Làm cách nào để giải câu đố này, điều này còn khá mơ hồ. Ngay cả nhà toán
học nổi tiếng Gauss C. F. vẫn chưa tìm ra được một lời giải đầy đủ khi ông xem xét câu đố này vào năm 1850. Điều thường xảy ra đối với các câu đố dường như là không có một cách nào có thể đưa ra các lời giải có được sự phân tích đầy đủ, mà chỉ có những lời giải được phát hiện một cách tình cờ do sự may mắn của một số lần áp dụng phương pháp thử sai, hoặc sau khi đã thực hiện một số lượng khổng lồ các phép tính. Hình 6.9 cho chúng ta hai phương án thỏa yêu cầu câu đố và cũng cho chúng ta tin rằng câu đố có lời giải.
Trong phần này, chúng ta sẽ phát triển hai chương trình để giải bài toán tám con hậu, đồng thời chúng ta cũng sẽ thấy được rằng, việc lựa chọn các cấu trúc dữ liệu có thể ảnh hưởng lên một chương trình đệ quy như thế nào.
6.3.1. Lời giải cho bài toán tám con hậu
Bất kỳ ai khi thử tìm lời giải cho bài toán tám con hậu thường ngay lập tức bị cuốn hút vào việc tìm cách đặt những con hậu lên bàn cờ, có thể là ngẫu nhiên, có thể theo một trật tự luận lý nào đó, nhưng dù cách nào đi nữa thì điều chắc chắn xảy ra là con hậu được đặt sau sẽ không bao giờ được nhìn thấy các con hậu đã được đặt trước đó. Bằng cách này, nếu may mắn, một người có thể đặt được cả
tám con hậu thỏa yêu cầu bài toán, và đó là một lời giải. Nếu không may, một hoặc nhiều con hậu sẽ phải được lấy đi để đặt lại vào những chỗ khác và việc tìm lời giải lại được tiếp tục.
Chúng ta sẽ viết một hàm đệ quy solve_from để giải bài toán này. Công việc cần làm tại một thời điểm (một trạng thái nào đó của bàn cờ mà số hậu chưa đủ) là:
• Đặt thêm một con hậu vào một vị trí hợp lệ.
• Gọi đệ quy để xử lý tương tự với số hậu cần xử lý tiếp đã giảm 1.
Lớp Queens dưới đây sẽ có một số phương thức cần thiết mà chúng ta sẽ bàn đến chi tiết sau. Ở đây chúng chỉ cần biết rằng đối tượng configuration của nó sẽ chứa một trạng thái của bàn cờ. Khi nó làm thông số cho lần đệ quy bên trong, nó đã có được thêm một con hậu hợp lệ. Trong lần gọi solve_from đầu tiên từ chương trình chính, số hậu cần giải quyết là 8 và bàn cờ chưa có hậu nào.
solve_from(Queens configuration)
{
1. if configuration Queens đã có tám con hậu
1. print configuration
2. else
1. for mỗi ô của bàn cờ mà chưa bị nhìn thấy bởi con hậu nào {
1. Đặt một con hậu lên ô p của configuration;
2. solve_from(configuration);
3. Lấy con hậu ra khỏi ô p của configuration;
}
}
Rõ ràng là sau mỗi bước đệ quy, kích thước bài toán giảm dần. Chúng ta có
điểm dừng của đệ quy là khi cả 8 con hậu đều đã tìm được vị trí thích hợp (lệnh rẽ nhánh if), hoặc khi không còn tìm được vị trí nào hợp lệ cho con hậu cần đặt tiếp nữa (trường hợp vòng lặp for đã quét hết các vị trí hợp lệ còn lại).
Việc đặt một con hậu ở một ô p chỉ là một bước thử nghiệm, chúng ta vẫn còn chưa thay đổi vị trí của nó trong khi mà chúng ta còn có thể tiếp tục đặt những con hậu khác cho đến khi đạt được cả 8 con. Và cũng giống như khi người ta làm bằng tay, khi không còn vị trí nào có thể đặt tiếp hậu, hàm solve_from cũng phải lấy đi những con hậu đã đặt (dòng lệnh 2.1.3) để tiếp tục thử với những vị trí hợp lệ khác (vòng lặp for sẽ lần lượt chuyển sang các vị trí này). Rõ ràng là nếu không thể tiếp tục đặt thêm một con hậu nào đó nữa thì việc quay lui là để thay đổi lần thử nghiệm vừa rồi sang một phương án khác để tiếp tục tìm lời giải. Tuy nhiên, giải thuật quay lui của chúng ta còn có một đặc điểm nữa là khi đã đạt được lời giải cho cả 8 con hậu, thì chương trình cũng vẫn quay lui, và việc quay lui này là để tìm thêm nhiều lời giải khác. Tóm lại, khi một lần gọi đệ quy bên trong
kết thúc, chương trình của chúng ta sẽ luôn lùi một bước để khảo sát tiếp các khả năng khác còn lại, và giải thuật sẽ cho đáp án là tất cả các lời giải của bài toán.
6.3.2. Ví dụ với bốn con Hậu
Chúng ta sẽ xét xem giải thuật trên được thực hiện như thế nào cho một trường hợp đơn giản, đó là bài toán đặt bốn con hậu lên bàn cờ 4x4, hình 6.10.
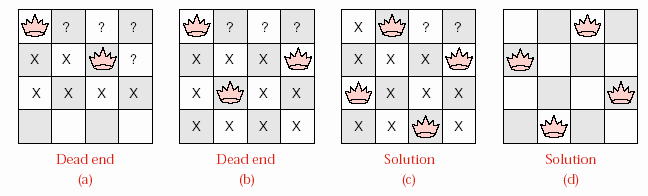
Hình 6.10 – Lời giải cho bài toán bốn con hậu
Chúng ta cần phải đặt mỗi con hậu lên một hàng của bàn cờ. Chúng ta luôn
bắt đầu thử từ ô cực trái còn hợp lệ của hàng. Ở hàng trên cùng chúng ta chọn ô ở góc trái (hình 6.10a). Các dấu hỏi đánh dấu những lựa chọn hợp lệ khác mà chúng
ta chưa thử đến. Trước khi thử các ô này, chúng ta chuyển sang hàng thứ hai. Hai ô đầu tiên đã bị nhìn thấy bởi con hậu ở hàng 1, chúng ta đánh dấu bằng dấu
chéo. Ô thứ 3 và thứ 4 còn tự do, chùng ta tiếp tục thử với ô thứ 3 và đáng dấu hỏi cho ô thứ 4. Tiếp theo chúng ta chuyển xuống hàng thứ 3, nhưng cả bốn ô ở hàng này đều đã bị nhìn thấy bởi một trong hai con hậu ở hai hàng trên. Xem
như chúng ta đã gặp điểm chết.
Khi gặp một điểm chết, chúng ta cần phải quay ngược lại và bỏ đi sự lựa chọn mới nhất để thử một khả năng khác. Trường hợp này thể hiện trong hình 6.10b), con hậu ở hàng thứ nhất không đổi nhưng con hậu ở hàng thứ hai đã được thử với vị trí còn lại là ô thứ 4 (ô thứ 3 vừa thử thất bại được đánh dấu chéo). Sau đó chúng ta thấy ở hàng thứ ba chỉ có ô thứ 2 là tự do, nhưng khi tiếp tục sang hàng thứ 4 thì cũng không còn ô nào tự do. Lúc này chúng ta lại gặp một điểm chết mới, chúng ta lại cần phải quay ngược lại.
Tại điểm này, quay ngược lên hàng trên, chúng ta thấy hàng thứ ba không còn khả năng lựa chọn nào, ngược lên hàng thứ hai cũng vậy. Do đó chúng ta phải quay ngược lên đến hàng thứ nhất, ô thử mới trong hàng này là ô thứ 2 (hình 6.10c). Khi đi xuống, chúng ta thấy hàng thứ hai chỉ có một khả năng lựa chọn, đó là ô thứ 4. Xuống hàng thứ ba chỉ có ô thứ 1 là tự do. Cuối cùng, ở hàng thứ tư có một ô tự do là ô 3. Tuy nhiên đây chỉ là một trường hợp thỏa yêu cầu
bài toán, mà chưa phải là một lời giải trọn vẹn cho bài toán đặt bốn con hậu lên bàn cờ 4x4.
Nếu muốn tìm mọi lời giải, chúng ta có thể tiếp tục bằng cách tương tự: quay ngược lại lần lựa chọn mới nhất để thử với khả năng tiếp theo. Trong hình 6.10c không còn lựa chọn nào khác ở hàng thứ tư, hàng thứ ba và hàng thứ hai. Do đó chúng ta ngược lên đến hàng thứ nhất, thử ô thứ 3. Lựa chọn này dẫn đến một lời giải duy nhất ở hình 6.10d.
Cuối cùng, khi thử với ô 4 ở hàng thứ nhất, chúng ta cũng không thu thêm một kết quả nào. Thực ra, cấu hình với con hậu ở ô 3 và con hậu ở ô 4 của hàng thứ nhất chính là hai hình ảnh ngược của ô 2 và ô 1 tương ứng. Nếu chúng ta đi từ trái sang phải trên hình 6.10c, chúng ta có được cấu hình ở hình 6.10d.
6.3.3. Phương pháp quay lui (Backtracking)
Phương pháp trên được gọi là giải thuật quay lui. Trong đó, việc tìm một lời giải đầy đủ được thực hiện bằng cách xây dựng các lời giải riêng phần sao cho chúng luôn thỏa những điều kiện của bài toán. Giải thuật được áp dụng để kéo dài một lời giải riêng phần cho thành một lời giải trọn vẹn. Tuy nhiên, tại một bước nào đó, nếu có sự vi phạm điều kiện của bài toán, giải thuật sẽ quay ngược trở lại, bỏ đi sự lựa chọn mới nhất để thử với một khả năng cho phép khác.
Giải thuật quay lui tỏ ra hiệu quả trong những trường hợp mà ban đầu tưởng như có rất nhiều khả năng lựa chọn, nhưng sau đó chỉ một số ít khả năng là còn sót lại sau tiến trình kiểm tra xa hơn. Trong các bài toán xếp thời khóa biểu, chẳng hạn trong việc tổ chức các vòng đấu thể thao, sự lựa chọn thời gian cho một số trận đấu ban đầu thường là rất dễ, nhưng càng về sau, các ràng buộc sẽ làm giảm đáng kể các khả năng có thể.
Phần tiếp theo đây chúng ta sẽ tìm hiểu cách hiện thực cụ thể cho bài toán con hậu cũng như một số chương trình liên quan đến các trò chơi, để thấy được ý tưởng đệ quy và giải thuật quay lui là cốt lõi của những bài toán ở dạng này.”
6.3.4. Phác thảo chung cho chương trình đặt các con hậu lên bàn cờ
6.3.4.1. Chương trình chính
Mặc dù chúng ta còn phải xác định rất nhiều chi tiết về cấu trúc dữ liệu để chứa các vị trí của các con hậu trên bàn cờ, nhưng ở đây chúng ta vẫn có thể viết trước chương trình chính để gọi hàm đệ quy mà chúng ta đã phác thảo.
Đầu tiên các thông tin về chương trình sẽ được in ra. Do việc kiểm tra chương trình với những bài toán nhỏ hơn là có ích, chẳng hạn với bài toán chỉ có bốn con hậu, chúng ta sẽ cho phép người sử dụng nhập vào số con hậu theo ý muốn. Đây cũng là kích thước của bàn cờ (board-size). Hằng số max_board sẽ được khai báo trong file queens.h.
int main()
/*
pre: Người sử dụng cần cho biết kích thước của bàn cờ. post: Mọi lời giải cho bài toán các con hậu đuợc in ra. uses: lớp Queens và hàm đệ quy solve_from.
*/
{
int board_size;
print_information();
cout << "What is the size of the board? " << flush;
cin >> board_size;
if (board_size < 0 || board_size > max_board)
cout << "The number must be between 0 and " << max_board << endl;
else {
Queens configuration(board_size); // Bàn cờ chưa có hậu nào.
solve_from(configuration);
}
}
6.3.4.2. Lớp Queens
Định nghĩa biến Queens configuration(board_size) dùng một constructor có thông số của lớp Queens để tạo một bàn cờ có kích thước theo sự lựa chọn của người sử dụng và khởi tạo một đối tượng Queens rỗng có tên là configuration. Đối tượng Queens rỗng này được gởi cho hàm đệ quy của chúng ta, trong đó các con hậu sẽ được đặt lần lượt lên bàn cờ.
Phác thảo trong phần 6.3.1 cho thấy lớp Queens cần các phương thức như in một trạng thái, thêm một con hậu vào một ô trên bàn cờ, lấy con hậu này đi, kiểm tra xem một ô nào đó có tự do hay không. Ngoài ra, để hiện thực hàm solve_from, lớp Queens cũng cần chứa dữ liệu là board_size để chứa kích thước bàn cờ cũng như thuộc tính count để đếm số con hậu đã được đặt lên bàn cờ.
Sau khi bắt đầu xây dựng một cấu hình, chúng ta sẽ tìm ô kế tiếp bằng cách nào? Ngay khi một con hậu vừa được đặt trong một hàng nào đó, không ai lại đi mất thì giờ vào việc tìm một vị trí khác cho con hậu mới cũng trên cùng hàng đó, do nó chắc chắn sẽ bị nhìn thấy bởi con hậu vừa đặt xong. Không thể có nhiều hơn một con hậu trong cùng một hàng. Mục đích của chúng ta là đặt cho được số con hậu được yêu cầu lên bàn cờ (board_size), và ở đây cũng chỉ có board_size
hàng. Do đó mỗi hàng phải có chính xác chỉ một con hậu. Đây là nguyên tắc tổ chim câu (pigeonhole principle): nếu chúng ta có n chú chim và n cái tổ và không cho phép nhiều hơn một con trong một tổ thì chúng ta chỉ có thể đặt mỗi con vào một tổ và phải dùng hết các tổ. Chúng ta có thể tiến hành bằng cách đặt các con hậu vào bàn cờ, mỗi lần cho một hàng, bắt đầu từ hàng số 0, như vậy count không chỉ là để đếm số hậu đã được đặt mà còn là chỉ số của hàng sẽ được đặt hậu kế tiếp.
Các đặc tả cho các phương thức của lớp Queens như sau:
bool unguarded(int col) const;
post: trả về true nếu ô thuộc hàng count (hàng đang được xử lý kế tiếp) và cột col không bị nhìn thấy bởi một con hậu nào khác; ngược lại trả về false.
void insert(int col);
pre: Ô tại hàng count và cột col không bị nhìn thấy bởi bất kỳ con hậu nào.
post: Một con hậu vừa được đặt vào ô tại hàng count và cột col, count tăng thêm 1.
void remove(int col);
pre: Ô tại hàng count-1 và cột col đang có một con hậu.
post: Con hậu trên được lấy đi, count giảm đi 1.
bool is_solved() const;
post: trả về true nếu số hậu đã đặt vào bàn cờ bằng với kích thước bàn cờ board_size; ngược
lại, trả về false.
6.3.4.3. Hàm đệ quy solve_from
Với các đặc tả trên hàm solve_from đã phác thảo trong phần trước đã được cụ thể hóa như sau. Tham số configuration được gởi tham chiếu do bên trong hàm có thay đổi nó.
void solve_from(Queens &configuration)
/*
pre: Bàn cờ đã chứa được count hậu hợp lệ tại hàng 0 đến hàng count -1.
post: n con hậu đã được đặt hợp lệ lên bàn cờ.
uses: lớp Queens và các hàm solve_from, recursively.
*/
{
if (configuration.is_solved()) configuration.print();
else
for (int col = 0; col < configuration.board_size; col++)
if (configuration.unguarded(col)) {
configuration.insert(col);
solve_from(configuration);// Gọi đệ quy tiếp để thêm các con hậu còn lại.
configuration.remove(col);
}
}
6.3.5. Tinh chế: Cấu trúc dữ liệu đầu tiên và các phương thức
Một cách hiển nhiên để hiện thực cấu hình Queens là lưu bàn cờ như một mảng hai chiều, mỗi phần tử biểu diễn việc có hay không một con hậu. Vậy mảng hai chiều là lựa chọn đầu tiên của chúng ta cho cấu trúc dữ liệu. Tập tin queens.h chứa định nghĩa sau:
const int max_board = 30;
class Queens {
public:
Queens(int size);
bool is_solved() const;
void print() const;
bool unguarded(int col) const;
void insert(int col);
void remove(int col);
int board_size; // Kích thước của bàn cờ bằng số hậu cần đặt.
private:
int count;//Chứa số hậu đã đặt được và cũng là chỉ số của hàng sẽ được đặt tiếp hậu.
bool queen_square[max_board][max_board];
};
Với cấu trúc dữ liệu này, phương thức thêm một con hậu dễ dàng như sau:
void Queens::insert(int col)
/*
pre: Ô tại hàng count và cột col không bị nhìn thấy bởi bất kỳ con hậu nào.
post: Một con hậu vừa được đặt vào ô tại hàng count và cột col, count tăng thêm 1.
*/
{
queen_square[count++][col] = true;
}
Các phương thức is_solved, remove, print cũng rất dễ và chúng ta xem
như bài tập.
Để khởi tạo cấu hình Queens, chúng ta cần constructor có thông số để đặt kích thước cho bàn cờ:
Queens::Queens(int size)
/*
post: Bàn cờ được khởi tạo chưa có hậu nào.
*/
{
board_size = size;
count = 0;
for (int row = 0; row < board_size; row++)
for (int col = 0; col < board_size; col++)
queen_square[row][col] = false;
}
Thuộc tính count khởi gán là 0 vì chưa có con hậu nào được đặt lên bàn cờ. Constructor này được thực hiện khi chúng ta vừa khai báo một đối tượng Queens trong chương trình chính.
Cuối cùng, chúng ta cần viết phương thức kiểm tra một ô tại một cột nào đó trên hàng đầu tiên chưa có hậu (xét từ trên xuống) có bị nhìn thấy bởi các con hậu đã có trên bàn cờ hay không. Chúng ta cần xét cột hiện tại và hai đường chéo đi qua ô này. Việc xét cột thật dễ dàng, còn việc xét đường chéo cần một số tính toán về chỉ số. Chúng ta hãy xem hình 6.11 cho trường hợp bàn cờ 4x4.
Chúng ta có thể gọi tên cho bốn hướng của hai đường chéo như sau: đường chéo trái-dưới (lower-left) hướng xuống dưới về bên trái, đường chéo phải-dưới (lower-right), đường chéo trái-trên (upper-left), và đường chéo phải trên (upper- right).
Trước tiên, chúng ta hãy xem xét đường chéo trái-trên ở hình 6.11c. Nếu chúng ta bắt đầu từ ô [row][col], các ô thuộc đường chéo trái-trên có toạ độ [row-i][col-i] với i là số nguyên dương. Đường chéo trái-trên này phải kết thúc khi gặp cạnh trên của bàn cờ (row-i==0) hoặc cạnh trái của bàn cờ (col- i==0). Chúng ta có thể dùng vòng lặp tăng i từ 1 cho đến khi row-i<0 hoặc col-i<0.
Chúng ta có thể làm tương tự cho ba đường chéo còn lại. Tuy nhiên, khi kiểm tra một ô có bị nhìn thấy bởi các con hậu hay không thì chúng ta không cần kiểm tra hai đường chéo dưới của ô này vì theo giải thuật các hàng dưới vẫn chưa có hậu.
bool Queens::unguarded(int col) const
/*
post: trả về true nếu ô thuộc hàng count (hàng đang được xử lý kế tiếp) và cột col không bị
nhìn thấy bởi một con hậu nào khác; ngược lại trả về false.
*/
{
int i;
bool ok = true; // sẽ được gán lại false nếu chúng ta tìm thấy hậu trên cùng cột hoặc đường chéo.
for (i = 0; ok && i < count; i++)
ok = !queen_square[i][col]; // kiểm tra phần trên của cột.
for (i = 1; ok && count - i >= 0 && col - i >= 0; i++)
ok = !queen_square[count - i][col - i]; // kiểm tra phần trên bên trái của đường chéo.
for (i = 1; ok && count - i >= 0 && col + i < board_size; i++)
ok = !queen_square[count - i][col + i]; // kiểm tra phần trên bên phải của đường chéo.
return ok;
}
6.3.6. Xem xét lại và tinh chế
Chương trình mà chúng ta vừa hoàn tất đáp ứng hoàn toàn cho bài toán tám con hậu. Kết quả chạy chương trình cho chúng ta 92 lời giải khác nhau. Tuy nhiên, với bàn cờ có kích thước lớn hơn, thời gian cần để chạy chương trình rất lớn. Bảng sau đây cho chúng ta một vài ví dụ:
|
Kích thước
|
|
8
|
9
|
10
|
11
|
12
|
13
|
|
Số lời giải
|
|
92
|
352
|
724
|
2680
|
14200
|
73712
|
|
Thời gian (second)
|
|
0.05
|
0.21
|
1.17
|
6.62
|
39.11
|
243.05
|
|
Thời gian cho một
(ms.)
|
lời giải
|
0.54
|
0.6
|
1.62
|
2.47
|
2.75
|
3.30
|
Như chúng ta thấy, số lượng lời giải tăng rất nhanh theo kích thước của bàn
cờ, và thời gian tăng còn nhanh hơn rất nhiều, do thời gian cho một lời giải cũng tăng theo kích thước bàn cờ. Nếu muốn giải cho các bàn cờ kích thước lớn, chúng
ta cần tìm một chương trình hiệu quả hơn.
Chúng ta hãy tìm xem vì sao chương trình của chúng ta chạy quá lâu như vậy. Việc gọi đệ quy và quay lui rõ ràng là chiếm nhiều thời gian, nhưng thời gian này lại phản ánh đúng phương pháp cơ bản mà chúng ta dùng để giải bài toán. Đó chính là bản chất của giải thuật và nó được lý giải bởi một số lượng lớn lời giải. Một số vòng lặp trong phương thức unguarded cũng đòi hỏi một lượng thời gian đáng kể. Chúng ta hãy thử xét xem có thể bỏ bớt một vài vòng lặp được chăng. Có cách nào để xét một ô có bị nhìn thấy bởi các con hậu hay không mà không phải xét hết các ô trên cùng cột và hai đường chéo bắc ngang?
Có một cách để thực hiện điều này, đó là cách thay đổi dữ liệu mà chúng ta lưu giữ trong mảng. Thay vì lưu thông tin các ô nào đã có các con hậu, chúng ta có thể dùng mảng để nắm giữ tất cả các ô đã bị các con hậu nhìn thấy. Từ đó, chúng ta sẽ dễ dàng hơn trong việc kiểm tra xem một ô có bị các con hậu nhìn thấy hay không. Một sự thay đổi nhỏ có thể giúp ích cho việc quay lui, bởi vì một ô có thể có nhiều hơn một con hậu nhìn thấy. Với mỗi ô, chúng ta có thể lưu một số để đếm số con hậu nhìn thấy nó. Khi một con hậu được thêm vào, chúng ta tăng biến đếm này thêm 1 cho tất cả các ô cùng hàng, cùng cột và trên hai đường chéo của nó. Ngược lại, khi lấy đi một con hậu, các biến đếm tương ứng này cũng cần giảm bớt 1.
Việc lập trình theo phương án này được dành lại như bài tập. Chúng ta nhận xét thêm rằng, tuy phương án mới này có chạy nhanh hơn chương trình đầu tiên nhưng vẫn còn một số vòng lặp để cập nhật lại các biến đếm vừa nêu. Suy nghĩ
thêm một chút nữa, chúng ta sẽ thấy rằng chúng ta có thể loại bỏ hoàn toàn các vòng lặp này.
Ý tưởng chính ở đây là việc nhận ra rằng mỗi hàng, mỗi cột, mỗi đường chéo trên bàn cờ đều chỉ có thể chứa nhiều nhất là một con hậu. (Nguyên tắc tổ chim câu cho thấy rằng, trong một lời giải, mọi hàng và mọi cột đều có con hậu, nhưng không phải mọi đường chéo đều có con hậu, do số đường chéo nhiều hơn số hàng và số cột.)
Từ đó, chúng ta có thể nắm giữ các ô chưa bị các con hậu nhìn thấy bằng cách sử dụng 3 mảng có các phần tử kiểu bool: col_free, upward_free, và downward_free, trong đó các đường chéo từ dưới lên và trái sang phải được gọi là upward, các đường chéo từ trên xuống và trái sang phải được gọi là downward (hình 6.11d và e). Do chúng ta đặt các con hậu lên bàn cờ mỗi lần tại một hàng, bắt đầu từ hàng 0, chúng ta không cần một mảng để biết được hàng nào còn trống.
Cuối cùng, để in một cấu hình, chúng ta cần biết số thứ tự của cột có chứa con hậu trong mỗi hàng, chúng ta sẽ dùng một mảng các số nguyên, mỗi phần tử dành cho một hàng và chứa số của cột chứa con hậu trong hàng đó.
Cho đến bây giờ, chúng ta đã có thể giải quyết trọn vẹn bài toán mà không cần đến mảng hai chiều biểu diễn bàn cờ như phương án đầu tiên nữa, và chúng ta cũng đã có thể loại mọi vòng lặp trừ các vòng lặp khởi tạo các trị ban đầu cho các mảng. Nhờ vậy, thời gian cần thiết để chạy chương trình mới này phản ánh một cách chặt chẽ số bước cần khảo sát trong phương pháp quay lui.
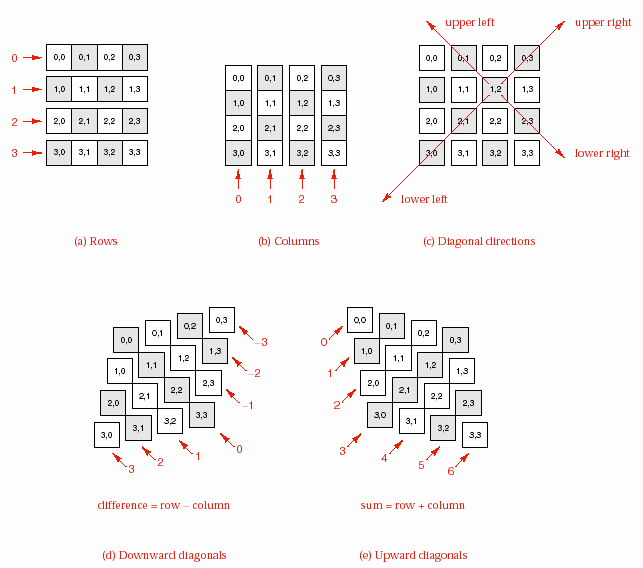
Hình 6.11 – Các chỉ số của các ô trong bàn cờ
Chúng ta sẽ đánh số cho các ô trong một đường chéo như thế nào? Chỉ số của
đường chéo upward dài nhất trong mảng hai chiều như sau:
[board_size-1][0],[board_size-2][1], ...,[0][board_size-1]
Đặc tính chung của các chỉ số này là tổng của hàng và cột luôn là (board_size–1). Điều này gợi ý rằng, như hình 6.11e, bất kỳ một đường chéo upward nào cũng có tổng của hàng và cột của mọi ô đều là một hằngsố. Tổng này bắt đầu từ 0 cho đường chéo upward có chiều dài là 1 tại góc trái trên cùng của mảng, cho đến(2xboard_size–2) cho đường chéo upward có chiều dài là 1 tại góc phải dưới cùng của mảng. Do đó chúng ta có thể đánh số cho các đường chéo upward từ 0 đến (2xboard_size–2), và như vậy, ô ở hàng i và cột j sẽ thuộc đường chéo upward có số thứ tự là i+j.
Bằng cách tương tự, như hình 6.11d, các đường chéo downward có hiệu giữa hàng và cột là một hằng số, từ (–board_size+1) đến (board_size–1). Các đường chéo downward sẽ được đánh số từ 0 đến (2xboard_size–1), một ô tại hàng i và cột j thuộc đường chéo downward có số thứ tự (i–j+board_size–1).
Sau khi đã có các chọn lựa trên chúng ta có định nghĩa mới cho lớp Queens
như sau:
class Queens {
public:
Queens(int size);
bool is_solved() const;
void print() const;
bool unguarded(int col) const;
void insert(int col); void remove(int col); int board_size;
private:
int count;
bool col_free[max_board];
bool upward_free[2 * max_board - 1];
bool downward_free[2 * max_board - 1];
int queen_in_row[max_board]; // số thứ tự của cột chứa hậu trong mỗi hàng.
};
Chúng ta sẽ hoàn tất chương trình qua việc hiện thực các phương thức cho lớp
mới. Đầu tiên là constructor khởi gán tất cả các trị cần thiết cho các mảng.
Queens::Queens(int size)
/*
post: The Queens object is set up as an empty
configuration on a chessboard with size squares in each row and column.
*/
{
board_size = size;
count = 0;
for (int i = 0; i < board_size; i++) col_free[i] = true;
for (int j = 0; j < (2*board_size -1); j++) upward_free[j] = true;
for (int k = 0; k < (2*board_size -1); k++) downward_free[k] = true;
}
Phương thức insert chỉ cần cập nhật cột và hai đường chéo đi ngang qua ô
tại [count][col] là đã bị nhìn thấy bởi con hậu mới thêm vào, các trị này cũng có thể là false sẵn trước đó do chúng đã bị các con hậu trước đó nhìn thấy.
void Queens::insert(int col)
/*
Pre: The square in the first unoccupied row (row count) and column col is not guarded by any queen.
Post: A queen has been inserted into the square at row count and column col; count has been incremented by 1.
*/
{
queen_in_row[count] = col;
col_free[col] = false;
upward_free[count + col] = false;
downward_free[count - col + board_size - 1] = false;
count++;
}
Cuối cùng phương thức unguarded chỉ cần kiểm tra cột và hai đường chéo đi
ngang qua ô tại [count][col] có bị các con hậu nhìn thấy hay chưa.
bool Queens::unguarded(int col) const
/*
Post: Returns true or false according as the square in the first
unoccupied row (row count) and column col is not guarded by any queen.
*/
{
return col_free[col]
&& upward_free[count + col]
&& downward_free[count - col + board_size - 1];
}
Chúng ta thấy rằng phương thức trên đơn giản hơn trong phương án đầu tiên của
nó rất nhiều. Các phương thức còn lại is_solved, remove, và print xem như bài tập. Bảng sau đây cho các con số nhận được từ chương trình cuối cùng này.
|
Kích thước
|
|
8
|
9
|
10
|
11
|
12
|
13
|
|
Số lời giải
|
|
92
|
352
|
724
|
2680
|
14200
|
73712
|
|
Thời gian (seconds)
|
|
0.01
|
0.05
|
0.22
|
1.06
|
5.94
|
34.44
|
|
Thời gian cho một
|
lời giải
|
0.11
|
0.14
|
0.30
|
0.39
|
0.42
|
0.47
|
|
(ms.)
|
|
|
|
|
|
|
|
Với trường hợp tám con hậu, chương trình mới chạy nhanh gấp 5 lần chương
trình cũ. Khi kích thước bàn cờ tăng lên tỉ lệ này còn cao hơn nữa, như trường hợp 13 con hậu, chương trình mới chạy nhanh gấp 7 lần chương trình cũ.
6.3.7. Phân tích về phương pháp quay lui
Chúng ta sẽ tổng kết phần này qua việc phỏng đoán tổng số các công việc mà chương trình của chúng ta phải làm.
6.3.7.1. Tính hiệu quả của phương pháp quay lui
Chúng ta bắt đầu bằng việc tính xem việc quay lui đã nhớ được bao nhiêu công việc so với tất cả các công việc có thể có. Xét trường hợp bàn cờ 8x8, nếu chúng ta tiếp cận bài toán một cách đơn giản bằng cách viết một chương trình tìm tất cả các phương án để xếp sao cho đủ tám con hậu lên bàn cờ rồi sau đó mới loại các
trường hợp không hợp lệ, với mỗi cấu hình là một sự lựa chọn 8 vị trí trong 64 vị trí, chúng ta có số cấu hình cần khảo sát lên đến:

 64
64
8 = 4,426,165,368.
Nếu chúng ta nhìn thấy được rằng mỗi hàng chỉ có thể có một con hậu thì số cấu hình cần thử giảm ngay xuống:
88 = 16,777,216.
Con số này vẫn còn rất lớn. Chúng ta tiếp tục cho rằng mỗi cột chỉ có thể có một con hậu, số lựa chọn các cột còn tự do trên mỗi hàng sẽ là 8, 7, ..., 1. Tổng số lựa chọn trên 8 hàng hoàn toàn có thể được xử lý bởi máy tính:
8! = 40,320.
và số trường hợp mà chương trình của chúng ta phải xem xét còn nhỏ hơn, do những ô ở hàng đang xét mà thuộc cùng đường chéo với các con hậu ở những hàng trên thì đã bị bỏ qua ngay lập tức.
Cách hoạt động của quá trình quay lui cho thấy tính hiệu quả của nó như sau: các vị trí đã được cho rằng không chấp nhận được sẽ ngăn cản sự khảo sát tiếp các đường đi vô ích sau đó.
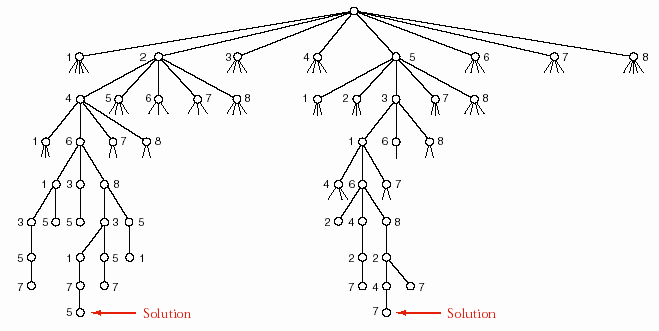
Hình 6.12 – Một phần của cây đệ quy cho bài toán tám con hậu
Một cách khác để biểu diễn hành vi của việc quay lui là việc xem xét cây đệ
quy của hàm đệ quy solve_from, hình 6.12 thể hiện một phần của cây này. Hai lời giải có trong hình tương ứng với hai lời giải trong hình 6.9. Mỗi nút trong cây có thể có tối đa là tám nút con tương ứng tám lần gọi đệ quy hàm solve_from với
tám trị hợp lệ của new_col. Tuy nhiên, ngay cả tại các mức gần với nút gốc, phần lớn các nhánh này đều được xác định sớm là không thỏa, và hiển nhiên rằng cứ mỗi nút cha không thỏa điều kiện của bài toán thì trong cây cũng không xuất hiện tiếp các nút con của nó. Phương pháp quay lui là một công cụ vô cùng hiệu quả để thu giảm một cây đệ quy về một kích thước có thể xử lý được.
6.3.7.2. Các cận dưới
Với bài toán n con hậu, tổng số công việc cần được thực hiệc bởi phương pháp quay lui tăng rất nhanh theo n. Chúng ta thử hình dung tốc độ tăng trưởng này nhanh đến cỡ nào. Khi đặt một con hậu vào một hàng trên bàn cờ, nó sẽ loại trừ nhiều nhất là ba vị trí ở hàng dưới (một vị trí cùng cột và hai vị trí chéo). Đối với hàng thứ nhất, việc quay lui sẽ khảo sát tất cả n vị trí. Ở hàng thứ hai, có ít nhất n-3 vị trí cần khảo sát; hàng thứ ba là n-6, và cứ thế. Vì vậy, để đặt các con hậu lên n/4 hàng đầu tiên, việc quay lui cần khảo sát ít nhất số vị trí:
n(n-3)(n-6)...(n-3n/4)
Tích này > (n/4)n/4do có tất cả n/4 thừa số và thừa số cuối cùng là n/4, các thừa số khác đều lớn hơn n/4. Để hình dung con số này tăng nhanh theo n như thế nào, chúng ta nhớ lại rằng bài toán tháp Hà Nội cần có 2n bước cho n đĩa, mà (n/4)n/4 còn tăng nhanh hơn 2n nhiều khi n tăng. Để thấy được điều này, chúng ta có:
log ((n/4)n/4) log (n/4)
⎯⎯⎯⎯⎯ = ⎯⎯⎯⎯
log (2n) 4 log (2)
Tỉ lệ này tăng không giới hạn khi n tăng. Chúng ta nói 2n tăng theo hàm mũ, còn (n/4)n/4 còn tăng nhanh hơn rất nhiều. Vậy với n lớn, chương trình áp dụng phương pháp quay lui cho bài toán tháp Hà Nội trên cũng sẽ chạy rất chậm.
6.3.7.3. Số lời giải
Chúng ta vẫn chưa chứng minh rằng việc in mọi lời giải cho bài toán n con hậu với n lớn là không thể thực hiện được bằng máy tính, mà chỉ mới chỉ ra rằng phương pháp quay lui là không thể làm được. Có thể còn một số giải thuật thông minh hơn nào đó có thể in các lời giải một cách nhanh chóng hơn giải thuật quay lui. Tuy nhiên, điều chúng ta quan tâm ở đây không phải là khả năng của máy tính mà là số lời giải thực sự của bài toán n con hậu. Điều đã có thể chứng minh được là số lời giải của bài toán này không thể được giới hạn bởi bất kỳ một đa thức bậc n nào. Thậm chí số lời giải này dường như còn không thể bị giới hạn bởi một biểu thức hàm mũ kn, với k là một hằng số, nhưng việc chứng minh điều này vẫn còn là một bài toán chưa có lời giải.
6.4. Các chương trình có cấu trúc cây: dự đoán trước trong các trò chơi
Trong các trò chơi trí tuệ, con người có thể dự đoán trước một số bước. Trong phần này chúng ta phát triển một giải thuật cho máy tính để tham gia các trò chơi có khảo sát trước một số bước đi. Chúng ta sẽ trình bày giải thuật qua hình ảnh của một cây và sử dụng đệ quy để lập trình cho cấu trúc này.
6.4.1. Các cây trò chơi
Chúng ta có thể vẽ ra các bước di chuyển có thể có qua hình ảnh của một cây trò chơi, trong đó gốc cây là trạng thái ban đầu, các cành xuất phát từ gốc là các bước đi hợp lệ của người chơi thứ nhất. Ở mức kế tiếp, các cành lại biểu diễn các bước đi hợp lệ của người chơi thứ hai tương ứng với mỗi cách đi của người thứ nhất, và cứ như thế. Nếu cho rằng mức của gốc là 0 thì các cành xuất phát từ các nút có mức chẵn biểu diễn bước đi của người thứ nhất, các cành xuất phát từ các nút có mức lẻ biểu diễn bước đi của người thứ hai.
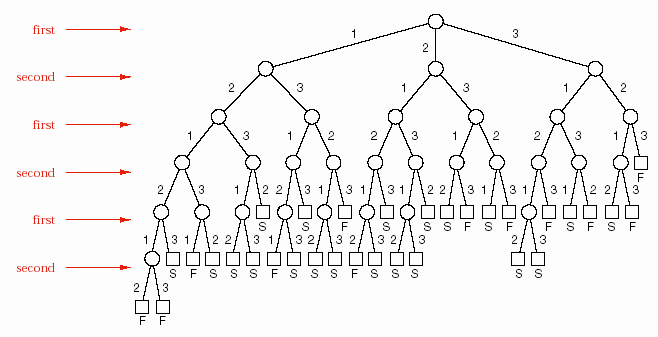
Hình 6.13 – Cây cho trò chơi số tám
Hình 6.13 là cây trò chơi đầy đủ của trò chơi Số tám. Trong trò chơi này,
người chơi thứ nhất sẽ lựa chọn một trong các số 1, 2, hoặc 3. Mỗi bước sau đó, mỗi người chơi sẽ được quyền chọn một trong ba số 1, 2, hoặc 3, nhưng không
được trùng với số mà người kia vừa chọn xong. Các cành trong cây mang con số
do người chơi chọn. Tổng các số được chọn sẽ được cộng tích lũy dần. Nếu đến lượt mình, người chơi chọn được con số làm cho tổng này đúng bằng tám thì sẽ là
người thắng cuộc; nếu tổng vượt quá tám thì người còn lại sẽ thắng. Trò chơi này
không có khả năng hòa. Trong sơ đồ, F có nghĩa là người thứ nhất thắng cuộc, và
S là người thứ hai thắng cuộc.
Ngay một trò chơi tầm thường như trò chơi Số tám trên đây cũng đã sinh ra một cây có kích thước không nhỏ. Các trò chơi thực sự hấp dẫn tựa như cờ vua còn có cây trò chơi lớn hơn rất nhiều, và chúng ta cũng không hy vọng gì vào việc có thể khảo sát hết các cành của nó. Như vậy, một chương trình chạy trong một thời gian cho phép chỉ có thể khảo sát một vài mức dưới một nút hiện tại của cây. Con người khi chơi những trò chơi này cũng không thể nhìn thấy được mọi khả năng phát triển cây cho đến khi trò chơi kết thúc, nhưng họ có thể có một số lựa chọn thông minh, bởi vì, theo kinh nghiệm, thông thường một người có thể nhận biết ngay một vài tình huống này là tốt hơn so với các tình huống khác, mặc dù họ cũng không bảo đảm được là sẽ thắng.
Đối với mọi trò chơi hấp dẫn mà chúng ta muốn chơi bằng máy tính, chúng ta cần một hàm gọi là hàm lượng giá để kiểm tra một tình huống hiện tại về mức độ thuận lợi của nó.
6.4.2. Phương pháp Minimax
Hình 6.14 là một cây con biểu diễn một phần của một cây trò chơi với mục đích minh họa cho bất kỳ trò chơi nào. Gốc cây con này biểu diễn vị trí hiện tại mà chúng ta đang muốn nhìn trước các bước đi. Chúng ta chỉ cần hàm lượng giá tại các nút lá của cây con này (đó là những vị trí mà chúng ta sẽ không nhìn tới trước xa hơn nữa), và từ các thông tin này, chúng ta phải chọn ra một cách đi cho vị trí hiện tại. Các nút lá trong cây được vẽ bằng hình vuông để phân biệt với các nút khác. Hình 6.14 chứa các trị cho các nút lá.
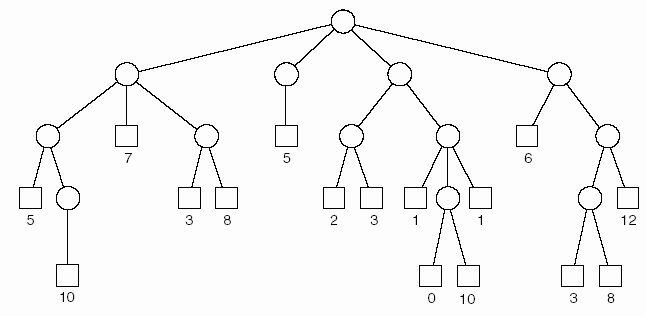
Hình 6.14 – Cây trò chơi với các trị được gán ở các nút lá
Bước đi mà chúng ta chọn sẽ là một trong các cành xuất phát từ gốc cây. Chúng ta dùng hàm lượng giá theo cách nhìn của người chơi sẽ thực hiện bước đi này. Giả sử gọi đó là người thứ nhất, người này sẽ chọn con số lớn nhất có thể. Tại bước kế, người chơi thứ hai lại chọn con số nhỏ nhất có thể, và cứ thế tiếp tục. Do hàm lượng giá được tính theo các tiêu chí dành cho người thứ nhất, nên giá trị nhỏ nhất của nó tương ứng tình huống xấu nhất của người thứ nhất. Giá trị này luôn được người thứ hai chọn vì theo khuynh hướng tình huống xấu nhất đối với người thứ nhất chính là tình huống tốt nhất của người thứ hai.Bằng cách đi ngược từ các nút lá lên, chúng ta có thể gán các trị cho mọi nút trong cây. Chúng ta hãy thực hiện việc này cho một phần của cây trong hình 6.14, bắt đầu từ cành bên trái nhất của cây. Nút đầu tiên chưa có nhãn là nút tròn nằm ngay trên nút hình vuông mang số 10. Do không có sự lựa chọn nào khác từ nút này nên nó cũng có số 10. Nút cha của nó có hai nút con mang số 5 và 10. Nút cha này thuộc mức thứ ba trong cây nên biểu diễn bước đi của người thứ nhất, đó là người ưu tiên chọn số lớn. Vậy người này đã chọn 10 nên nút cha này cũng sẽ mang trị 10.
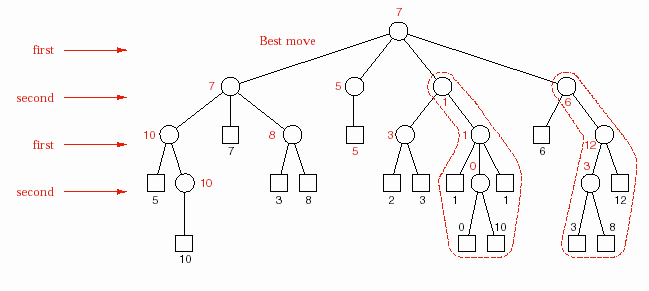
Hình 6.15 – Lượng giá theo phương pháp Minimax cho cây trò chơi
Chúng ta tiếp tục chuyển lên mức trên. Ở đây nút cha có ba nút con, con thứ
nhất từ trái sang là 10, con thứ hai là 7, con thứ ba là số lớn được chọn ra từ 3 và
8 nên là 8. Đây là mức chơi của người thứ hai, do đó trị nhỏ nhất trong ba trị trên được chọn, đó là 7. Cứ như thế, nếu tiếp tục chúng ta sẽ có được cây ở hình
6.15. Trị của vị trí hiện tại này là 7, và người chơi hiện tại, là người chơi thứ
nhất theo hình vẽ, sẽ chọn cành bên trái nhất của vị trí hiện tại này.
Trong việc đánh giá cây trò chơi này, chúng ta đã luân phiên chọn số nhỏ nhất (minima) và số lớn nhất (maxima). Do đó quá trình này còn gọi là phương pháp minimax.
6.4.3. Phát triển giải thuật
Chúng ta sẽ xem xét bằng cách nào mà phương pháp minimax có thể được lồng trong một giải thuật hình thức để dự đoán trước trong các chương trình trò chơi. Chúng ta sẽ viết một giải thuật tổng quát để có thể sử dụng trong bất kỳ một trò chơi nào có hai người chơi.
Chương trình sẽ cần truy xuất đến thông tin về một trò chơi cụ thể nào đó mà chúng ta muốn chơi. Chúng ta giả sử rằng thông tin này được tập hợp trong hiện thực của hai lớp gọi là Move và Board. Một đối tượng của lớp Move biểu diễn một bước đi của trò chơi, và một đối tượng của lớp Board biểu diễn một tình huống của trò chơi. Sau này chúng ta sẽ hiện thực các phiên bản của hai lớp trên đây cho trò chơi Tic-Tac-Toe.
Đối với lớp Move, chúng ta chỉ cần phương thức constructor: một constructor để tạo đối tượng Move theo ý của người chơi, và một constructor khác để tạo một đối tượng Move rỗng. Chúng ta cũng giả sử rằng các đối tượng của lớp Move và lớp Board đều có thể được gởi bằng tham trị cho hàm cũng như có thể được sử dụng phép gán một cách an toàn, do đó chúng ta cần viết đầy đủ toán tử gán định nghĩa lại (overloaded assignment operator) và copy constructor cho cả hai lớp.
Đối với lớp Board, các phương thức cần có là: khởi tạo đối tượng, kiểm tra trò chơi đã kết thúc hay chưa, tiến hành một bước đi nhận được qua tham trị, đánh giá một tình huống, và cung cấp một danh sách các nước đi hợp lệ hiện tại.
Phương thức legal_moves, trả về các nước đi hợp lệ hiện tại, sẽ cần một danh sách các thông số để tính toán các kết quả. Chúng ta cần một sự lựa chọn giữa các hiện thực của cấu trúc dữ liệu list để chứa các cách đi này. Trong việc nhìn tới trước, thứ tự giữa các cách đi mà chúng ta sẽ khảo sát là không quan trọng, do đó chúng có thể được lưu trong bất kỳ dạng nào của list. Để đơn giản cho việc lập trình, chúng ta sẽ sử dụng ngăn xếp. Phần tử của ngăn xếp sẽ là các đối tượng Move. Chúng ta cần định nghĩa:
typedef Move Stack_entry;
Chúng ta cần thêm hai phương thức để hỗ trợ trong việc lựa chọn nước đi tốt nhất trong số các nước đi hợp lệ. Phương thức đầu tiên, gọi là better, sử dụng hai thông số là hai số nguyên và trả về một kết quả khác 0 nếu người chơi chọn nước đi theo thông số thứ nhất, hoặc bằng 0 nếu người chơi chọn nước đi theo thông số thứ hai. Phương thức thứ hai, gọi là worst_case, trả về một hằng số được xác định trước có trị thấp hơn tất cả các trị mà hàm lượng giá tính được trong quá trình nhìn trước.
Chúng ta có định nghĩa của lớp Board như sau:
class Board {
public:
Board();//constructor khởi tạo trạng thái ban đầu thích hợp đối với mỗi trò chơi. int done() const; // kiểm tra xem trò chơi đã kết thúc hay chưa. void play(Move try_it);
int evaluate() const;
int legal_moves(Stack &moves) const;
int worst_case() const;
int better(int value, int old_value) const; // chọn nước đi tốt nhất.
void print() const;
void instructions() const;
/* Các phương thức, hàm và dữ liệu bổ sung tùy từng trò chơi cụ thể */
};
Đối tượng Board cần lưu một tình huống của trò chơi và người mà sắp thực hiện bước đi.
Trước khi viết hàm nhìn trước để đánh giá cây trò chơi, chúng ta cần chọn ra số bước mà giải thuật nhìn trước sẽ phải khảo sát. Đối với một trò chơi tương đối phức tạp, chúng ta cần định ra độ sâu (depth) sẽ được nhìn trước, các mức bên dưới nữa sẽ không được xét đến. Một điều kiện dừng khác của việc nhìn trước chính là khi trò chơi kết thúc, đó là lúc mà phương thức done của Board trả về true. Nhiệm vụ chính của việc nhìn trước trong cây có thể được mô tả bởi giải thuật đệ quy sau đây:
Algorithm look_ahead (thông số là một đối tượng Board);
1. if đệ quy dừng (độ sâu depth == 0 hoặc game.done())
1. return trị lượng giá của tình huống
2. else
1. for mỗi nước đi Move hợp lệ
1. tạo một đối tượng Board mới bằng cách thực hiện nước đi Move.
2. gọi đệ quy look_ahead tương ứng với sự lựa chọn tốt nhất của người chơi kế tiếp;
2. Chọn cách đi tốt nhất cho người chơi trong số các cách đi tìm được trong vòng lặp trên;
3. return đối tượng Move tương ứng và trị;
6.4.4. Tinh chế
Chương trình cụ thể của giải thuật trên như sau:
int look_ahead(const Board &game, int depth, Move &recommended)
/*
pre: đối tượng Board biểu diễn một tình huống hợp lệ của trò chơi.
post: các nước đi của trò chơi được nhìn trước với độ sâu là depth, nước đi tốt nhất được chỉ ra trong tham biến recommended.
uses: các lớp Stack, Board, và Move, cùng với hàm look_ahead một cách đệ quy.
*/
{
if (game.done() || depth == 0)
return game.evaluate();
else {
Stack moves;
game.legal_moves(moves);
int value, best_value = game.worst_case();
while (!moves.empty()) { Move try_it, reply; moves.top(try_it); Board new_game = game; new_game.play(try_it);
value = look_ahead(new_game, depth - 1, reply);
if (game.better(value, best_value)) { // nước đi thử try_it vừa rồi hiện là tốt nhất.
best_value = value;
recommended = try_it;
}
moves.pop();
}
return best_value;
}
}
Tham biến recommended sẽ nhận về một nước đi được tiến cử (trừ khi đệ quy
rơi vào điểm dừng, đó là khi trò chơi kết thúc hoặc độ sâu của việc nhìn trước depth bằng 0). Do chúng ta không muốn đối tượng game bị thay đổi trong hàm, đồng thời để tránh việc chép lại mất thời gian, nó được gởi cho hàm bằng tham chiếu hằng. Chúng ta cũng lưu ý rằng việc khai báo tham chiếu hằng này chỉ hợp lệ khi đối tượng game trong hàm chỉ thực hiện các phương thức đã được khai báo const trong định nghĩa của lớp Board.
6.4.5. Tic-Tac-Toe
Như trên đã nói, hàm đệ quy look_ahead cùng hai lớp Board và Move trên đây tuy rất đơn giản, nhưng nó lại là cốt lõi trong các chương trình biểu diễn trò chơi có hai đối thủ. Chúng ta sẽ triển khai phác thảo này trong trò chơi tic-tac-toe rất quen thuộc. Để làm được điều này, cả hai lớp sẽ chứa thêm một ít dữ liệu khác so với hiện thực hình thức ban đầu.
Việc viết chương trình chính hoàn tất cùng hàm look_ahead cho trò chơi tic- tac-toe được dành lại như bài tập. Chương trình có thể chứa thêm nhiều chức năng như cho phép người chơi với máy, đưa ra các phân tích đầy đủ cho mỗi tình huống, cung cấp chức năng cho hai người chơi với nhau, đánh giá các bước đi của hai đối thủ,...
Chúng ta biểu diễn lưới trò chơi tic-tac-toe bằng một mảng 3x3 các số nguyên, ô có trị 0 là ô trống, trị 1 và 2 biểu diễn nước đi của người thứ nhất và thứ hai tương ứng.
Trong đối tượng Move, chúng ta chứa tọa độ các ô trên lưới. Một nước đi hợp lệ chứa tọa độ có các trị từ 0 đến 2. Chúng ta không cần đến tính đóng kín của đối tượng Move vì nó chỉ như một vật chứa để chứa các giá trị.
// lớp move cho trò chơi tic-tac-toe
class Move {
public: Move();
Move(int r, int c);
int row;
int col;
};
Move::Move()
/*
post: đối tượng Move được khởi tạo bởi trị mặc định không hợp lệ.
*/
{
row = 3;
col = 3;
}
Move::Move(int r, int c)
/*
post: đối tượng Move được khởi tạo bởi toạ độ cho trước.
*/
{
row = r;
col = c;
}
Lớp Board cần một constructor để khởi tạo trò chơi, phương thức print và
instruction (in các thông tin cho người chơi), phương thức done, play và legal_moves (hiện thực các quy tắc chơi), và các phương thức evaluate, better, và worst_case (phán đoán điểm cho các nước đi khác nhau). Chúng ta còn có thể bổ sung hàm phụ trợ the_winner cho biết rằng trò chơi đã có người thắng chưa và người thắng là ai.
Lớp Board cần chứa thông tin về trạng thái hiện tại của trò chơi trong mảng
3x3 và tổng số bước đi đã thực hiện. Chúng ta có lớp Board như sau:
class Board {
public: Board();
bool done() const;
void print() const;
void instructions() const;
bool better(int value, int old_value) const;
void play(Move try_it);
int worst_case() const;
int evaluate() const;
int legal_moves(Stack &moves) const;
private:
int squares[3][3];
int moves_done;
int the_winner() const;
};
Constructor đơn giản chỉ làm một việc là khởi tạo tất cả các ô của mảng là 0
để chỉ rằng cả hai người chơi đều chưa đi nước nào.
Board::Board()
/*
post: đối tượng Board được khởi tạo rỗng tương ứng trạng thái ban đầu của trò chơi.
*/
{
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
squares[i][j] = 0;
moves_done = 0;
}
Chúng ta dành các phương thức in các thông tin cho người chơi như là bài tập.
Thay vào đó, chúng ta tập trung vào các phương thức liên quan đến các quy tắc của trò chơi. Để thực hiện một nước đi, chúng ta chỉ cần gán lại trị cho một ô và
tăng biến đếm moves_done lên 1. Dựa vào biến đếm này chúng ta còn biết được
đến lượt người nào đi.
void Board::play(Move try_it)
/*
post: nước đi try_it được thực hiện
*/
{
squares[try_it.row][try_it.col] = moves_done % 2 + 1;
moves_done++;
}
Hàm phụ trợ the_winner trả về một số khác không nếu đã có người thắng.
int Board::the_winner() const
/*
post: trả về 0 nếu chưa ai thắng; 1 nếu người thứ nhất thắng; 2 nếu người thứ hai thắng.
*/
{
int i;
for (i = 0; i < 3; i++)
if (squares[i][0] && squares[i][0] == squares[i][1]
&& squares[i][0] == squares[i][2])
return squares[i][0];
for (i = 0; i < 3; i++)
if (squares[0][i] && squares[0][i] == squares[1][i]
&& squares[0][i] == squares[2][i])
return squares[0][i];
if (squares[0][0] && squares[0][0] == squares[1][1]
&& squares[0][0] == squares[2][2])
return squares[0][0];
if (squares[0][2] && squares[0][2] == squares[1][1]
&& squares[2][0] == squares[0][2])
return squares[0][2];
return 0;
}
Trò chơi kết thúc sau 9 nước đi hoặc khi có người thắng. (Chương trình của chúng ta không phát hiện sớm khả năng hòa trước khi kết thúc 9 nước đi).
bool Board::done() const
/*
post: trả về true nếu trò chơi đã phân thắng bại hoặc cả 9 ô trên bàn cờ đã được đánh dấu, ngược lại trả về false.
*/
{
return moves_done == 9 || the_winner() > 0;
}
Trong trò chơi đơn giản này, nước đi hợp lệ là những ô mang trị 0.
int Board::legal_moves(Stack &moves) const
/*
post: Thông số moves chứa các nước đi hợp lệ.
*/
{
int count = 0;
while (!moves.empty()) moves.pop();
for (int i = 0; i < 3; i++)
for (int j = 0; j < 3; j++)
if (squares[i][j] == 0) {
Move can_play(i,j); moves.push(can_play); count++;
}
return count;
}
Chúng ta chuyển sang các phương thức có thể cho những sự đánh giá về một
tình huống của trò chơi hoặc của một nước đi có thể xảy ra. Chúng ta sẽ bắt đầu đánh giá một tình huống của trò chơi là 0 trong trường hợp chưa có người nào
thắng. Nếu một trong hai người thắng, chúng ta sẽ đánh giá tình huống dựa vào
quy tắc: càng thắng nhanh thì càng hay. Điều này cũng đồng nghĩa với việc càng thua nhanh thì càng dở. Nếu moves_done là số nước đi cả hai người chơi đã thực hiện thì (10-moves_done) càng lớn khi số nước đã đi càng nhỏ, tương ứng sự đánh giá cao khi người thứ nhất sớm thắng. Ngược lại, nếu người thứ hai thắng thì chúng ta dùng trị (moves_done-10), số nước đi càng nhỏ thì trị này là một số càng âm, tương ứng việc thua nhanh chóng của người thứ nhất là rất dở.
Dĩ nhiên rằng, cách đánh giá này chỉ được áp lên điểm cuối của việc nhìn trước (ở độ sâu mong muốn hoặc khi trò chơi đã phân thắng bại). Trong phần lớn các tình huống, nếu chúng ta nhìn trước càng xa thì bản chất chưa tinh của cách đánh giá sẽ đỡ gây hậu quả xấu hơn.
int Board::evaluate() const
/*
post: trả về 0 khi chưa có người thắng cuộc; hoăc 1 số dương từ 1 đến 9 trong trường hợp người thứ nhất thắng, ngược lại là một số âm từ –1 đến –9 trong trường hợp người thứ hai thắng.
*/
{
int winner = the_winner();
if (winner == 1) return 10 - moves_done;
else if (winner == 2) return moves_done - 10;
else return 0;
}
Phương thức worst_case có thể chỉ đơn giản trả về một trong hai trị 10 hoặc
-10, do evaluate luôn trả một trị nằm giữa -9 và 9. Từ đó, phương thức so sánh
better chỉ cần so sánh một cặp số nguyên có trị nằm giữa -10 và 10. Các phương thức này xem như bài tập.
Giờ thì chúng ta đã phác thảo xong phần lớn chương trình trò chơi tic-tac-toe. Một chương trình lấy độ sâu cho việc nhìn trước là 9 sẽ chơi tốt do chúng ta luôn có thể nhìn trước đến một tình huống mà sự đánh giá về nó là chính xác. Một chương trình nhìn trước với một độ sâu không lớn có thể mắc phải sai lầm, do nó có thể kết thúc việc nhìn trước bởi tập các tình huống có trị đánh giá bằng 0 một cách nhầm lẫn.